| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 공유경제
- 엘뱌키안
- 정형데이터
- F분포
- 영어연설
- PGTM
- CC#3
- 대중연설
- Public Speaking
- 임상통계
- CC#5
- 평창
- 데분
- 연설
- SQLD
- 토스트마스터
- 사이허브
- 카이제곱분포
- 분석
- publicspeaking
- 데이터
- 풀러스
- Toastmaster
- 취업
- 제약
- 인과추론
- 데이터분석
- 2018계획
- 영화
- 구글#빅쿼리#데이터분석
- Today
- Total
지지플랏의 DataScience
(16) DSforS: Chap 7: 클러스터링(k-means,계층, GMMs) 본문
이번글은 데이터 과학을 위한 통계 마지막 단원이자 내용인 클러스터링에 대해서 배운다. 크게는 k-평균클러스터링과 계층적 클러스터링, 모델 기반의 클러스터링의 원리와 차이 적용 방법에 대해서 기술한다.
1. 책 목차
- 7.2. k-평균클러스터링
- 7.2.1. 간단한예제
- 7.2.2. k-평균 알고리즘
- 7.2.3. 클러스터해석
- 7.2.4. 클러스터 개수 선정
- 7.3. 계층적 클러스터링
- 7.3.1.과 간단한 예제
- 7.3.2. 덴드로그램
- 7.3.3. 병합 알고리즘
- 7.3.4. 비유사도 측정
- 7.4. 모델 기반 클러스터링
- 7.4.1. 다변량 정규분포
- 7.4.2. 정규 혼합
- 7.4.3. 클러스터 개수 결정하기
- 7.5. 스케일링과 범주형 변수
- 7.5.1. 변수 스케일링
- 7.5.2. 지배 변수
- 7.5.3. 범주형 데이터와 고워거리
- 7.5.4. 혼납 데이터의 클러스터링 문제
2. 본문
비지도학습(UnSupervised Learning)은 데이터의 레이블(Y변수, 종속변수)가 없는 상황에서 데이터의 패턴이나 구조를 찾는 머신러닝의 한 방법이다. 지도학습과 달리 정답이 없기 때문에 난이도는 높지만 고객 세그멘테이션 분석 등 활용도가 높은 특징이 있다. 대표적으로 전 글에서 다뤘던 차원축소(ex PCA), 군집화(ex k-평균), 연관 규칙 학습(ex 장바구니 분석) 등이 있다. 본 글에서는 군집화에 대해서 다뤄본다.

2.1. k-평균 클러스터링 알고리즘
클러스터링(Clustering) 군집화의 개념은 측정 가능한 지표를 바탕으로 집단을 묶겠다는 의미이다. 대표적인 클러스터링은 Kmeans 클러스터링이다. 아이디어는 다음과 같다.
1. 초기 클러스터링 중심 설정
- k개의 클러스터 수를 선택
- 무작위로 k 개의 초기 클러스터 중심 u1,u2,...uk 를 선택
2. 할당 단계
- 각 데이터 포인트 xi를 가장 가까운 클러스터 중심에 할당
ci=argmin
- x_{i}: 데이터 포인트 i
- \mu_{i}: 클러스터 j의 중심
- x_{i} - \mu_{j} 는 데이터 포인트와 클러스터 중심 사이의 유클리드 거리
- \arg\min_{j}는 데이터 포인트와 클러스터 중심 들 사이 거리 중 최소 거리를 찾기 위한 인덱스 j를 반환한다는 의미

3. 업데이트 단계
- 각 클러스터 j에 대해 클러스터에 속한 데이터 포인트의 평균을 계산하여 새로운 클러스터 중심으로 설정
\mu_{j} = \frac{1}{|C_{j}|} \sum_{x_{i} \in C_{j}} x_{i}
4. 반복
- 2-3번을 를 클러스토의 중심 변화가 거의 없을 때 까지 반복
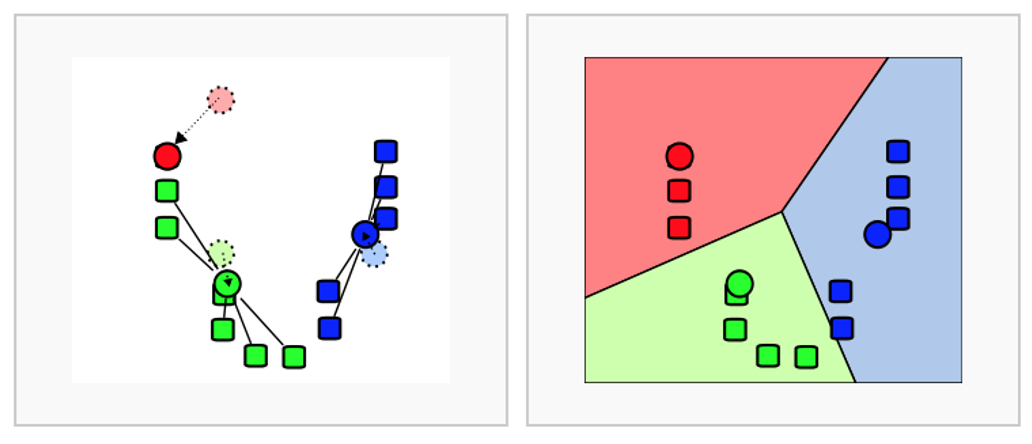
k-평균 클러스터링의 장점은 일반적으로 적용하기 쉽다 하지만 거리기반으로 가까움을 측정하기 때문에 차원이 많을 수록 정확도가 떨어진다. 또한 몇 개의 군집(k)를 선정할 것인지 주관적이며, 평균을 이용하기 때문에 이상치에 취약한 단점으로 가지고 있다.
2.2. 계층적 클러스터링
2.2.1. 계층적 클러스터링 알고리즘
계층적 클러스터링(Hierarchical Clustering)은 데이터를 계층 구조로 클러스터링 하는 방법으로 병합형과 분할형이 있다. 일반적인 병합형 계층적 클러스터링은 각 데이터 포인트를 개별 클러스터로 시작하여 점직적으로 클러스터를 병합해 나가는 방법이다. 마치 snake 게임 처럼 데이터를 합쳐 나간다고 생각하면 편하다. 알고리즘은 다음과 같다.
1. 초기화
- 각 데이터 포인트를 개별 클러스터로 간주. 따라서 n개의 클러스터 존재
2. 거리 계산
- 모든 클러스트 쌍 거리를 계산(ex 유클리드, 맨해튼, 코사인 유사도 등)
3. 클러스터 병합
- 가까운 클러스터를 병합 병합된 클러스터의 거리를 다시 계산함. 이때 클러스터간의 거리를 다시 계산하는 방법은 4가지가 있다.
- 단일 연결법(Single Linkage): 두 클러스터 간의 가장 짧은 거리를 기준으로 병합
- 완전 연결법(Complete Linkage): 두 클러스터 간의 가장 긴 거리를 기준으로 병합
- 평균 연결법(Average Linkage): 두 클러스터 간의 평균 거리를 기준으로 병합
- 중심 연결법(Centroid Linkage): 두 클러스터 중심 간의 거리를 기준으로 병합
4. 반복
- 모든 데이터 포인트가 하나의 클러스터로 병합될 때 까지 2-3단계 방법
5. 덴드로그램 생성
- 병합과정에서 클러스트의 형성을 시각화한 덴드로그램(dendrogram)*을 생성함.
*덴드로그램은 클러스터의 형성과 계층 구조를 나타내는 트리 형태의 다이어그램
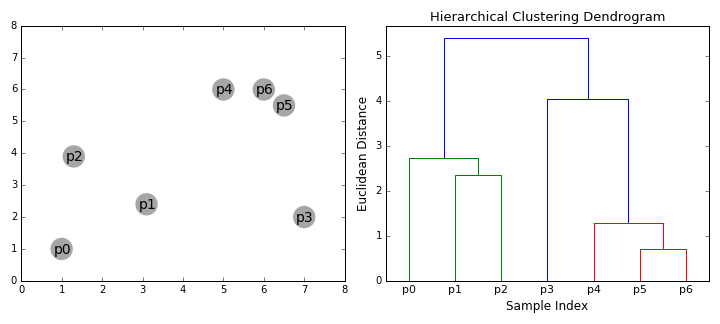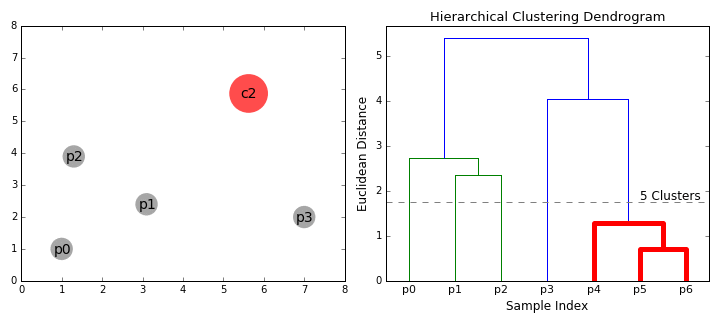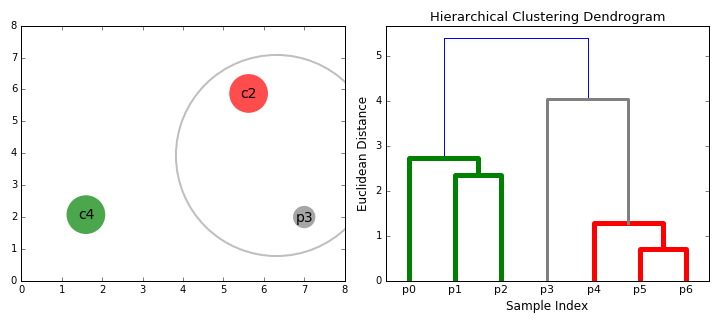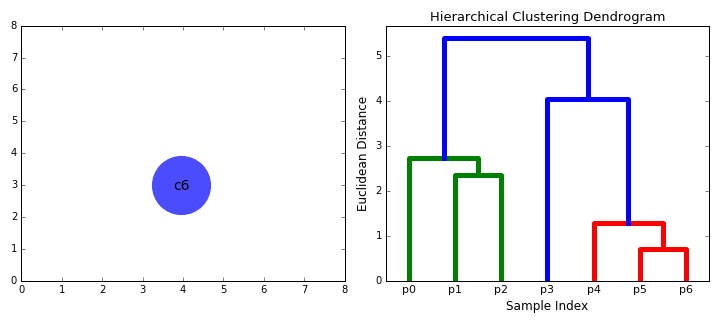
2.2.2. 덴드로그램
계층적 클러스터링은 트리 모델과 같이 자연스러운 시각적 표현이 가능하며 이를 덴드로그램(Dendrogram)이라고 한다. 흔히 마주할 수 있는 덴드로그램의 대표적인 예시는 생물 분류이다. 이렇게하면 각 군집에 어디에 속하는지 그리고 공통점과 차이점을 볼 수 있는 장점이 있다.
덴드로그램은 트리와 동일하게 Node, Branch, Root, Leat 의 구성요소로 이루어져 있다.
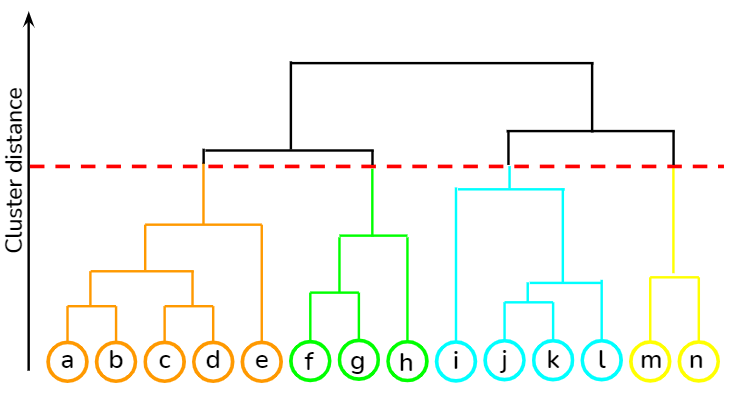
덴드로그램의 장점은 데이터의 계층적 구조를 직관적으로 파악할 수 있으며 클러스터 수를 시각적으로 설정할 수 있다는 장점이 있다. 위의 예시에서 보면 4가지의 수평 점선을 이용해 4가지 군집을 분류한 것을 볼 수 있다. 하지만 데이터가 크면 덴드로그램에 복잡해지며 수평축은 임의로 설정되는 것이라 절대적 의미를 해석하기 어렵다는 단점이 있다.
2.3. 모델기반 클러스터링
k-평균과 계층적 클러스터링 방법들은 확률모형에 기대지 않는 휴리스틱한 방법이라고 할 수 있다. 반면 모델기반 클러스터링은 데이터가 특정 확률 분포를 따르는 것으로 가정하여 클러스터링을 수행하는 방법이다. 대표적으로 가우시안혼합모델(Gaussian Mixture Models, GMMs)이 있다.
2.3.1 GMMs 정의
GMMs이라고 불리는 가우시안 혼합 모델은 말 그대로 정규분포를 여러 개 혼합하여 데이터의 복잡한 분포를 근사하기 위한 머신러닝 알고리즘이다.
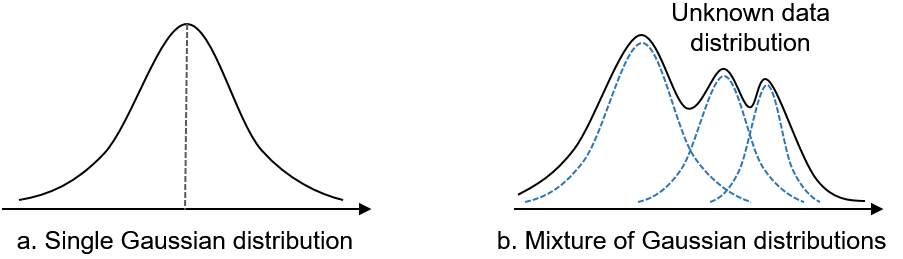
GMMs은 다음과 같은 가정을 한다.
- 데이터는 여러 개의 가우시안 분포로 부터 생성됨.
- 각 가우시안 분포는 특정 평균(\mu)와 공분산행렬(\sum)을 가지며, 이들의 가중치 합으로 전체 데이터 분포가 형성됨
식으로 풀자면 다음과 같다.
p(\mathbf{x}) = \sum_{k=1}^{K} \pi_k \mathcal{N}(\mathbf{x}; \mu_k, \Sigma_k)
- p(\mathbf{x}): 데이터 포인트 x의 확률 밀도 함수
- \pi_k: 가우시안 분포의 혼합 계수. 각 가우시안 분포가 전체 모델에서 차지하는 비율 .
- 단, \sum_{k=1}^{K}{\pi_{k} = 1} 및 0 <= \pi_{k} <= 1
- {N}(\mathbf{x}; \mu_k, \Sigma_k): 평균 \mu_{k}와 공분산 행렬 \Sigma_{k}를 가지는 k번째 가우시안 분포. 데이터 포인트 \mathbf{x} 가 k번째 가우시안 분포로부터 생성될 확률 밀도를 나타냄
- \mu_{k}: k번째 가우시안 분포의 평균 벡터
- \Sigma_{k}: k번째 가우시안 분포의 공분산 행렬
일반적인 1차원 정규분포인 경우 N(\mu, \sigma^{2})처럼 나타내지만 다차원의 경우 위처럼 (\Sigma) 공분산 행렬을 이용한다. GMM을 학습 시킨 다는 것은 주어진 데이터 셋 \chi = {x_{1}, x_{2}, .. x_{N}} 에 대해서 데이터의 확률 p(x)를 최대화 하는 매개변수 \theta = {\pi_{1}, .. \pi{K}, \mu_{1}, .. \mu_{K}, \Sigma_{1}, ... \Sigma_{K}} 를 추정하는 것과 같다.
2.3.2 GMMs의 학습방법 - 최대 우도 추정
GMMs을 학습하는 방법에는 최대 우도 추정, 최대 사후 확률 추정, 베이즈 추정, 변분 추청, MCMC 방법이 있다. 그중 최대 우도추정(MLE)는 확률 모델의 매개변수를 최적화 하기 위해서 머신러닝에서 가장 일반적으로 이용되는 방법 중 하나이며 로지스틱회귀에서도 적합하기 위하여 사용된다.
L(\mathcal{X}; \theta) = \log p(\mathcal{X}; \theta) = \log \prod_{n=1}^{N} p(\mathbf{x}_n; \theta)
- L(\mathcal{X}; \theta): 로그 가능도 함수(Log-likelihood function). 주어진 mathcal{X}와 매개변수 \theta에 대한 로그 가능도를 나타난다.
- p(\mathcal{X}; \theta): 전체 데이터 \mathcal{X}가 매개변수 \theta 하에서 관찰될 확률(우도, likelihood)
- p(x_{n} ; \theta): 개별 데이터 포인트 X_{n}가 매개 변수 \theta에서 관찰될 확률(우도, likelihood)
MLE 방법은 위 식을 최대화하도록 모델을 학습시킨다. GMMS에서는 데이터의 분포 p(x)를 K개의 가우시안분포의 혼합으로 가정하였으로 GMMs 학습을 위해 최대화해야하는 로그-가능도는 최종적으로 다음과 같다.
L(\mathcal{X}; \theta) = \sum_{n=1}^{N} \log \left( \sum_{k=1}^{K} \pi_k \mathcal{N}(\mathbf{x}_n; \mu_k, \Sigma_k) \right)
우리의 목적은 L(\mathcal{X}, \theta)를 최대화하는 \pi_{k}, \mu_{k}, \Sigma_{k}를 찾는 것이다. K개의 가우시안 분포마다 있으므로 매개변수는 총 3K가 된다. 결국 L(\mathcal{X}; \theta)를 최대화하는 매개변수를 찾는다는 것은 주어진 데이터가 나타내는 분포를 가장 잘 근사하는 모델 매개변수를 찾는 다는 것이다. 하지만 로그함수 내에 가우시안 분포의 합이 존재하여 MLE방법으로는 직접적으로 매개변수를 찾기 어렵다. 따라서 EM 알고리즘이 필요해졌다.
2.3.3. GMMs의 학습방법 2 - EM 알고리즘
GMMs는 주어진 데이터에 대해서 모델의 파라미터(평균,공분산 행렬, 혼합계수)를 추정하는 과정이다. 일반적으로 기대값-최대화(EM)알고리즘을 사용하며 절차는 다음과 같다.
- 초기화
- 초기 매개변수 \theta = (\pi_{k}, \mu_{k}, \Sigma_{k})를 설정
- Expectation 단계: 현재 파라미터 추정치를 바탕으로 각 데이터 포인트가 각 가우시안 분포에 속할 확률(책임도)을 계산
- \gamma(z_{nk}) = \frac{\pi_k \mathcal{N}(x_n \mid \mu_k, \Sigma_k)}{\sum_{j=1}^{K} \pi_j \mathcal{N}(x_n \mid \mu_j, \Sigma_j)}
책임도는 각 데이터 포인트가 특정 클러스터에 속할 확률을 계산하여 이는 k-평균 클러스터링이 하는 하드 클러스터링이 아닌 소프트 클러스터링을 한다고 말한다.
3. Maximization 단계: 책임도를 바탕으로 파라미터를 업데이트
- 새로운 혼합 계수: \pi_k = \frac{1}{N} \sum_{n=1}^{N} \gamma(z_{nk})
- 새로운 평균: \mu_k = \frac{\sum_{n=1}^{N} \gamma(z_{nk}) x_n}{\sum_{n=1}^{N} \gamma(z_{nk})}
- 새로운 공분산: \Sigma_k = \frac{\sum_{n=1}^{N} \gamma(z_{nk}) (x_n - \mu_k)(x_n - \mu_k)^T}{\sum_{n=1}^{N} \gamma(z_{nk})}
자세히보면 혼합 계수(모델의 가중치)는 각 가우시안 분포가 전체 데이터에서 차지하는 비율을 나태난다. 또한 평균은 책임도로 가중된 가중 평균으로 계산되며, 공분산은 각 클러스터에 데이터 포인터의 책임도로 가중된 공분산이다.
위 과정을 수렴할 때까지 반복한다. 굉장히 복잡해 보이는데 간략하게 요약하자면
- K개의 가우시안 분포가 혼합되어 있으므로 기존 MLE 방법으로는 모델의 파라미터를 직접 추정하는데 어렵다.
- 이를 이용해 기대값- 최대화(E-M) 알고리즘을 사용한다.
- E단계에서는 각 데이터 포인트가 각 가우시안 분포에 속할 확률을 계산하며 이를 책임도라고 한다.
- M단계에서는 책임도를 이용하여 혼합계수, 평균, 공분산을 계산한다.
2.3.4. GMMs의 Python 구현
import numpy as np
import matplotlib.pyplot as plt
from sklearn.mixture import GaussianMixture
# 샘플 데이터 생성
np.random.seed(0)
X = np.random.randn(300, 2)
# GMM 모델 피팅
gmm = GaussianMixture(n_components=3, random_state=0)
gmm.fit(X)
# 클러스터 할당 및 중심 계산
labels = gmm.predict(X)
centroids = gmm.means_
# 시각화
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis')
plt.scatter(centroids[:, 0], centroids[:, 1], s=100, c='red')
plt.title('GMM Clustering')
plt.show()
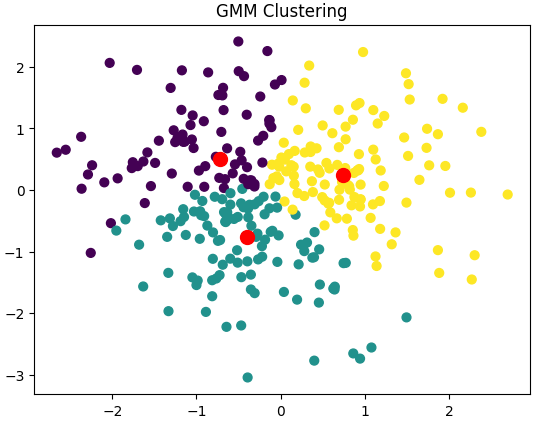
2.4. 클러스터링 평가 지표
2.4.1. Elbow 메소드
elbow메소드는 클러스터 수 k를 변화시키면서 각 k에 대한 비용함수를 계산하며 최적의 k를 선정하는 방법이다. 일반적으로 비용함수는 SSE(sum of Squared Error)를 사용하며 군집 수 가 증가함에 따라(즉 k가 증가함에 따라) SSE가 급격히 감소하다가 완만해지는 팔꿈치 지점을 찾아 최적의 클러스터 k 수를 찾게 된다. 절차는 다음과 같다.

- 클러스터 수행
- 각 k에 대해서 SSE 계산
\text{SSE} = \sum_{i=1}^{n}min_{\mu_{j}} \| x - \mu_i \|^2
3. k와 SSE를 그래프로 그려서, SSE의 감소가 완만해지는 지점 찾기
하지만 k값의 정하는 것을 도움을 주는 방법이지 데이터에 따라 Elbow 지점이 명확하지 않을 수 있을 수 있다는 점을 알아두면 좋다. 그밖에도 Calinski-Harabasz Index(군집 내 응집도와 군집 간 분리도 동시 고려) Davis-Bouldin Index(각 클러스터 분산과 클러스터 간의 거리 비율 평가), Dunn Index(클러스터간의 최소 거리와 내 최대 거리 평가) 하는 방법 들이 있다.
2.4.2. 실루엣 계수
비지도 학습 특성상 답이 없기 떄문에 평가를 하긴 어렵다. 하지만 군집화가 잘되었다는 평가로 다른 군집간의 거리는 멀리, 동일한 군집끼리는 가까이 있다는 아이디어로 지표를 만들어 볼 수 있다. 이를 실루엣 계수(silhouette analysis)로 평가할 수 있다.
S(i) = \frac{b(i) - a(i)}{max(a(i)),b(i))}, 단 i 는 데이터
- S(i) 가 1에 가까울수록 잘 클러스터링 됨
- S(i) 가 0에 가까울수록 데이터가 두 클러스터의 경계에 있음
- S(i) 가 -1에 가까울수록 데이터 포인트가 잘못 클러스터링 됨
실루엣 계수는 k-평균 클러스터링 뿐 아니라 계층적 클러스터링, DBSCAN, GMM 등 클러스터링 알고리즘에 적용할 수 있다.
3. 출처
- 머신러닝/확률모델 [머신러닝] 가우시안 혼합 모델 (Gaussian Mixture Model, GMM)과 EM 알고리즘
- Unsupervised Learning using Scikit Learn - Machine Learning with Python:
- https://www.datanovia.com/en/lessons/agglomerative-hierarchical-clustering
'Data Science > 데이터과학을 위한 통계' 카테고리의 다른 글
| [데이터 과학을 위한 통계] 책 리뷰와 KPT 회고 (2) | 2024.07.02 |
|---|---|
| (14) DSforS: Chap6. 6.3 배깅과 랜덤포레스트~ 6.4.부스팅 (0) | 2024.06.26 |
| (13)DSforS: Chap6. 6.2 트리 모델 - 정보이득개념 (0) | 2024.06.23 |
| (12) DSforS: Chap6. 6.1. k-최근접 이웃, 거리지표(마할라노비스) (0) | 2024.06.16 |
| (11) DSforS : Chap5 5.5 불균형 데이터 다루기 (0) | 2024.06.16 |




