데이터 과학통계 1.1. ~ 1.4.에서는 탐색적 데이터분석의 사례를 소개한다.
- 1.1 정형화된 데이터의 요소
- 1.2 테이블 데이터
- 1.3 위치 추정
- 1.4. 변이추정
1. 용어 정리
데이터과학을 처음 마주할 때 가장 곤란한 사실은 같은 의미를 다른 용어로 쓸 때가 있다는 것이다. 데이터를 레코드라고 하기도하며, 레코드는 2차원 테이블의 행을 뜻한다. 혹은 관측치라고도 부른다.

2차원 테이블에서 세로축을 열이라고 부르기도 차원 혹은 변수라고 부르기도한다. 이는 데이터과학이라는 학문이 통계학과 컴퓨터공학의 2가지 나무에서 성장하여 만난 학문이기 때문이다. 그 때문인지 본 책에서는 용어를 통일하려는 노력을 많이한다.
1.1 정형화된 데이터의 요소
- 연속형 데이터: 구간형, 실수형, 수치형 데이터
- 이산형 데이터: 정수형, 횟수 데이터
- 범주형 데이터: 목록, 열거, 요인, 명목, 다항형(polychotomous) 데이터
- 이진형 데이터: 이항적, 논리형, 지표, 불리언(boolean)데이터
- 순서형 데이터: 정렬된 요인 데이터
1.2 테이블 데이터
- 데이터 프레임: 테이블 데이터
- 피처: 특징, 속성, 입력, 예측변수
- 결과: 종속변수, 응답, 목표, 출력
- 레코드: 기록값, 사건, 사례, 예제, 관측값, 패턴 샘플
1.3 위치 추정
- 평균(mean): , average
- 가중평균( weighted mean ): weighted average
- 중간값(median): 50번째 백분위수(percentile)
- 가중 중간값(weighted median):
- 절사 평균(trimmed mean): 절단 평균(truncated mean)
- 로버스트하다(robust): 저항하다, 강건하다
- 특이값(outlier): 극단값
1.4. 변이추정
- 편차(deviation): 오차, 잔차
- 분산(variance): 평균제곱, 오차
- 표준편차(standard deviation)
- 평균절대편차(mean absolute deviation): L1 norm, 맨해튼 norm
- 중간값의 중위절대편차(MAD, mean absolute from the median)
- 범위(range)
- 순서통계량(order statistics): 순위
- 백분위수(percentile): 분위수
- 사분위범위(IQR, Interquantile range)
2. 가중치의 활용성
이상치의단점으로 인해 평균이 대표성이 약해진다는 것은 널리 알려진 사실이다. 이를 보완하기 위한 가중평균은 어떤경우에 잘사용되는지 궁금해졌다.
- 가중평균의 활용
중학교 남자의 평균점수가 30점이고 여자의 평균점수가 50점이라면 전체 평균점수는 40점인가? 이는 산술평균의 큰 함정이다. 두 값을 1:1로 생각하고 평균을 내려면 남자와 여자의 수가 같다는 전제가 있어야한다. 따라서 가중평균을 사용할 필요성이 있다. 즉 더 무거운 무게중심에 보정을 해주는 것이다.
- 가중평균 = 남자 학생의 평균점수 x 남자학생의 비율 + 여자학생의 평균점수 x 여자학생의 비율
여기서 남학생과 여학생의 비율의 합은 1이 되는 것이 합리적일 것이다.
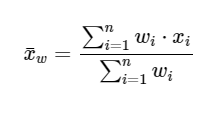
- 가중 통계량의 장단점
장점
- 데이터별 가중치를 반영하여 합리적인 통게량 제공
- 가중치를 이용한 패턴 발굴
- 이상치에 덜 민감
- 구현이 쉬움
단점
- 어떤 가중치가 더 좋은 것인지 판단하는 작업이 필요(주관)
3. 조화평균의 활용성
평균에는 산술평균 기하평균 조화평균이 있다. 대부분 산술평균을 평균이라는 대명사로 쓰긴 하지만 실제로이런 산술평균이 잘 먹히지 않는 경우가 있다.

A지점과 B지점를 왕복하는데 걸리는 시간을 계산해보고자 한다. 갈때 6km/h 올때 12km/h로 온다고 했으니 각각 2시간,1시간이 걸려 총 3시간이 걸린다.
반면 산술평균을 이용해서 9km/h 평균속도를 구하고 24km를 나누면 2.7시간이 나온다. 산술평균은 이처럼 비율의 평균을 구하는데 적합하지 않다. 이 경우 조화평균을 이용하여 계산하면 정답이 도출된다.

조화 평균은 머신러닝에서 분류문제를 평가하는 F1-score에서도 등장한다. F1 score는 실제 정답데이터를 맞춘 비율(재현율)과 정답을예측한 데이터를 맞춘비율(정밀도) 2가지 지표를 고려한다.
이경우 산술평균을 이용하면 둘 중 하나의 지표가 압도적으로 좋아 극단값으로 작용하면 실제 반대 지표가 높지 않음에도 과대평가될 위험이 있다. 이를 위해서 조화평균을 사용하게 된다. 조화평균은 기본적으로 비율의 평균을 낼때 사용하게 되며 둘 중 하나의 값이 극단값이라고해도 전체 값은 변동이 덜한편이다. 반면 두 지표가 모두 높거나 혹은 낮을때 잘 작동하는 특징이 있다.
출처:
데이터 과학을 위한 통계 : 데이터 분석에서 머신러닝까지 파이썬과 R로 살펴보는 50가지 핵심 개
데이터 과학의 관점에서 통계 핵심 개념과 기법을 필요한 것만 골라 소개한다. 50가지 개념을 차근차근 정리하고 코드를 실행해보면, 필수 통계 지식을 빠르게 흡수할 수 있다. 2판에는 기존 R 코
www.aladin.co.kr
for PSAT 자료해석: 가중평균 이론과 활용
PSAT 자료해석에 수학이 필요없다는 글을 썼지만, 그렇다고 수학을 전혀 모르는 사람이 필요한 스킬을 아는 사람과 똑같은 퍼포먼스를 낼 수는 없는 법이다. 꼭 알아야 하는 '기본기'에 해당하는
psat-bamdori.tistory.com
- https://zephyrus1111.tistory.com/309https://ballpen.blog/%EC%82%B0%EC%88%A0-%EA%B8%B0%ED%95%98-%EC%A1%B0%ED%99%94-%ED%8F%89%EA%B7%A0-%EA%B0%9C%EB%85%90-%ED%99%9C%EC%9A%A9/
평균 - 산술, 기하, 조화 평균의 개념과 실생활 활용 - ilovemyage
평균 공식에는 산술, 기하, 조화 평균이 있습니다. 보통 산술 평균을 이용하나 때로는 기하나 조화 평균을 사용하기도 합니다. 이러한 평균의 개념과 실생활에서의 활용 사례를 소개합니다. 아
ballpen.blog
'Data Science > 데이터과학을 위한 통계' 카테고리의 다른 글
| (6) DSforS : Chap 3 통계적 실험과 유의성 검정 3.4 ~ 3.8. (0) | 2024.05.27 |
|---|---|
| (5) DSforS : Chap 3 통계적 실험과 유의성 검정 3.1 ~ 3.3. (0) | 2024.05.22 |
| (4) DSforS : Chap 2 탐색적 데이터분석 2.4 ~ 2.8 (6) | 2024.05.20 |
| (3) DSforS : Chap 2 탐색적 데이터분석 2.4 ~ 2.8 (1) | 2024.05.15 |
| (2) DSforS : Chap 1 탐색적 데이터분석 1.5 ~ 2.3 (2) | 2024.05.13 |