집앞의 횡단보도를 자주 지나가는데, 횡단보도를 기다릴지 아닐지 늘 고민하면서 지나갑니다.'4명 기다리고 있는데 금방 바뀌지 않을까? 좀 더 가서 사거리에서 건너는게 나을까?' 저는 데이터를 수집해서 언제쯤 횡단보도가 바뀌는지, 그리고 이를 활용할 수 있는 분포는 뭐가 있는지 확인해보자는 문제의식을 정의하고 해결하는 방법을 작성했습니다. 월간 데이터노트 4기의 스터디로 진행된 분석입니다. 월간 데이터노트 참여에 관심이 있다면 다음 공지를 확인해주세요!
1. 주변상황 정보


- 횡단보도 기준 동편에는 1710세대, 서편에는 1068세대의 아파트 단지
- 횡단보도 바로 앞에 카페, 빠리바게트 등의 소규모 상가가 있으며, 도서관은 현재 운영 X
- 북쪽에 역시 대단지, 남쪽에는 공공기관이 있음
- 횡단보도를 이용하는 사람은 주민, 학생, 출퇴근 직장인들이 주류를 이루며, 10시/ 4시 정도에는 일부 유모차를 동반한 엄마가 등장
2. 데이터 수집
- 4차선도로이며 횡단보도 기준 빨간불 2분, 파란불 25초
- 제가 주로 이동하는 시간인 출퇴근/점심시간/퇴근 시간에 수시로 22개 수기 수집

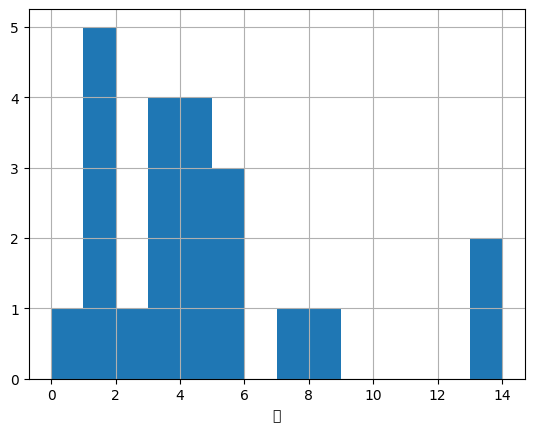
- 평균 4.1명, 중위 3.5, 표준편차 3.6명, IQR 기준 이상치 2개(13, 14)

- 시간대 분포

3. 분포 모델 검토
처음에는 포아송 분포라고 생각하고 호기심 발제했음
- 포아송 분포
- 정의: 일정 시간 & 공간 내에 독립적으로 발생하는 사건의 횟수를 모델링
- 분포의 특징과 적합성 체크
- 사건은 서로 독립적으로 발생 → 맞음
- 사건은 동시에 발생하지 않음 → 동시에 사람들이 도착하기도 함
- 평균 발생률은 관측 구간 내 일정 → 맞음
- 분산/평균의 값이 1임 → 아님 3.01임 (과산포임)
다른 조건이 어느정도 맞으나 분산과 평균이 같지 않아서 Claude가 음이항 분포를 추천함
- 음이항 분포
- 정의: r번째 성공을 관측할 때 까지 필요한 시행 횟수나 성공 확률이 p인 베르누이 시행에서 r번의 성공을 관측할때까지 실패한 횟수의 분포
- 분포의 특징과 적합성 체크
- 분산이 평균보다 큰 과산포(overdispersion) 데이터에 적합
- Ex) 특정 지역의 범죄 발생 건수(범죄가 특정 지역에 집중)
- Ex2) 소비자 구매 행동(일부 고객이 훨씬 더 자주 구매)
- 분산이 평균보다 큰 과산포(overdispersion) 데이터에 적합
- 데이터에 과산포가 존재(분산> 평균) → 맞음
- 사건 발생이 군집화 되는 경향이 있음 → 맞음 일부시간대 몰림
- 개체별로 발생률에 차이가 있음 → 있을 수 있음(주부/학생 등)
- 발생 확률이 시간에 따라 변할 수 있음 → 그러함
4. 분석
- 히스토그램 및 분포 시각화
- 포아송 분포와 음이항 분포 적합
- 적합도 검정 (카이제곱 검정)
- AIC 및 BIC를 사용한 모델 비교
import matplotlib.pyplot as plt
import platform
def set_matplotlib_font():
system = platform.system()
if system == "Windows":
plt.rc('font', family='Malgun Gothic')
elif system == "Darwin": # macOS
plt.rc('font', family='AppleGothic')
elif system == "Linux":
plt.rc('font', family='NanumGothic')
else:
print("Unknown system. Please set font manually.")
plt.rcParams['axes.unicode_minus'] = False
# 폰트 설정 함수 호출
set_matplotlib_font()
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import scipy.stats as stats
from statsmodels.discrete.discrete_model import Poisson, NegativeBinomial
df = data.copy()
df.columns = ['timestamp','count']
print("데이터 샘플:")
print(df.head())
# 기본 통계량
print("\n기본 통계량:")
print(df['count'].describe())
mean_count = df['count'].mean()
var_count = df['count'].var()
print(f"평균: {mean_count:.4f}")
print(f"분산: {var_count:.4f}")
print(f"분산/평균 비율: {var_count/mean_count:.4f}")
# 히스토그램 및 분포 시각화
plt.figure(figsize=(12, 6))
# 히스토그램
plt.subplot(1, 2, 1)
# sns.histplot(df['count'], kde=True, stat='density', discrete=True)
df['count'].hist(density = True)
plt.title('횡단보도 건너는 사람 수 히스토그램')
plt.xlabel('사람 수')
plt.ylabel('빈도')
# 경험적 분포와 이론적 분포 비교
x = np.arange(0, df['count'].max() + 1)
# 포아송 분포 확률 질량 함수
poisson_pmf = stats.poisson.pmf(x, mean_count)
# 음이항 분포 매개변수 추정
# 방법 1: 모멘트 방법
r = mean_count**2 / (var_count - mean_count) if var_count > mean_count else 100
p = mean_count / var_count if var_count > mean_count else mean_count / (mean_count + 1)
# 음이항 분포 확률 질량 함수
nb_pmf = stats.nbinom.pmf(x, r, p)
plt.subplot(1, 2, 2)
plt.bar(x, [df['count'].value_counts().get(i, 0) / len(df) for i in x], alpha=0.5, label='실제 데이터')
plt.plot(x, poisson_pmf, 'ro-', label=f'포아송 분포 (λ={mean_count:.2f})')
plt.plot(x, nb_pmf, 'go-', label=f'음이항 분포 (r={r:.2f}, p={p:.2f})')
plt.title('경험적 분포와 이론적 분포 비교')
plt.xlabel('사람 수')
plt.ylabel('확률')
plt.legend()
plt.tight_layout()
# 포아송 분포 적합도 검정 (카이제곱 검정)
observed = np.zeros(df['count'].max() + 1)
for i in range(len(observed)):
observed[i] = df['count'].value_counts().get(i, 0)
expected = len(df) * stats.poisson.pmf(np.arange(len(observed)), mean_count)
# 카이제곱 값 계산
# 기대빈도가 5 미만인 셀은 통합
min_expected = 5
observed_adj = []
expected_adj = []
last_obs = 0
last_exp = 0
for obs, exp in zip(observed, expected):
if exp >= min_expected:
observed_adj.append(obs)
expected_adj.append(exp)
else:
last_obs += obs
last_exp += exp
if last_exp > 0:
observed_adj.append(last_obs)
expected_adj.append(last_exp)
observed_adj = np.array(observed_adj)
expected_adj = np.array(expected_adj)
chi2 = np.sum((observed_adj - expected_adj) ** 2 / expected_adj)
df_chi2 = len(observed_adj) - 1 - 1 # 매개변수 1개 추정 (자유도 = 셀 수 - 1 - 추정된 매개변수 수)
p_value = 1 - stats.chi2.cdf(chi2, df_chi2) if df_chi2 > 0 else None
print("\n포아송 분포 적합도 검정 (카이제곱 검정):")
print(f"카이제곱 값: {chi2:.4f}")
print(f"자유도: {df_chi2}")
print(f"p-value: {p_value if p_value is not None else '자유도가 0 이하'}")
print(f"결론: {'포아송 분포에 적합하지 않음 (p < 0.05)' if p_value is not None and p_value < 0.05 else '포아송 분포에 적합함 (p >= 0.05)' if p_value is not None else '검정 불가 (자유도 부족)'}")
# AIC 및 BIC를 사용한 모델 비교
# 인공 변수를 만들어 모델 적합 (상수 모델)
X = np.ones((len(df), 1))
y = df['count'].values
# 포아송 회귀 모델
poisson_model = Poisson(y, X)
poisson_results = poisson_model.fit(disp=0)
# 음이항 회귀 모델
try:
nb_model = NegativeBinomial(y, X)
nb_results = nb_model.fit(disp=0)
print("\n모델 비교 (AIC 및 BIC):")
print(f"포아송 모델 AIC: {poisson_results.aic:.4f}")
print(f"음이항 모델 AIC: {nb_results.aic:.4f}")
print(f"포아송 모델 BIC: {poisson_results.bic:.4f}")
print(f"음이항 모델 BIC: {nb_results.bic:.4f}")
print(f"더 적합한 모델: {'음이항 분포' if nb_results.aic < poisson_results.aic else '포아송 분포'} (AIC 기준)")
except:
print("\n음이항 회귀 모델을 적합할 수 없습니다. 데이터가 충분하지 않거나 모델이 수렴하지 않습니다.")
# 시간대별 분석
df['hour'] = df['timestamp'].dt.hour
df['time_of_day'] = pd.cut(df['hour'],
bins=[0, 12, 18, 24],
labels=['아침(0-12시)', '오후(12-18시)', '저녁(18-24시)'],
include_lowest=True)
time_stats = df.groupby('time_of_day')['count'].agg(['mean', 'var', 'count'])
time_stats['var/mean'] = time_stats['var'] / time_stats['mean']
print("\n시간대별 통계:")
print(time_stats)
# 시간대별 분포 시각화
plt.figure(figsize=(10, 6))
sns.boxplot(x='time_of_day', y='count', data=df)
plt.title('시간대별 횡단보도 건너는 사람 수 분포')
plt.xlabel('시간대')
plt.ylabel('사람 수')
plt.tight_layout()
plt.show()
# 결론
print("\n분포 분석 결론:")
if var_count > mean_count:
print(f"분산({var_count:.4f})이 평균({mean_count:.4f})보다 크므로 과산포(overdispersion)가 존재합니다.")
print("따라서 포아송 분포보다 음이항 분포가 더 적합할 수 있습니다.")
elif var_count < mean_count:
print(f"분산({var_count:.4f})이 평균({mean_count:.4f})보다 작으므로 과소산포(underdispersion)가 존재합니다.")
print("이 경우 포아송 분포보다 이항 분포가 더 적합할 수 있습니다.")
else:
print(f"분산({var_count:.4f})이 평균({mean_count:.4f})과 거의 같으므로 포아송 분포에 적합합니다.")
- 모델 비교 (AIC 및 BIC) -> 더 적합한 모델: 음이항 분포 (AIC 기준)
- 포아송 모델 AIC: 126.3588
- 음이항 모델 AIC: 111.9646
- 포아송 모델 BIC: 127.4498
- 음이항 모델 BIC: 114.1467
- 모수 추정 방법: 모먼트 방법과 최대 우도 추정법 존재
- 모멘트 방법
# 데이터의 평균과 분산 계산
mean = np.mean(data)
var = np.var(data, ddof=1) # 표본 분산
# 모수 추정
p = mean / var
r = mean * p / (1 - p)5. 결론
- 눈으로 보기엔 포아송 분포가 더 잘 맞는거같은데 AIC기준으로는 음이항 분포가 더 잘맞다고 한다.
- 카이제곱을 검정을 쓰는 이유는 관측된 빈도와 분포의 기대 빈도와 비교하는 방법이기 떄문
- AIC/BIC가 사용된 이유는 다른 통계 모델의 상대적 품질을 비교하는 지표이기 때문(상대적 평가)
- 음이항 분포의 모수
- r(성공 횟수): 1.94
- p(성공 확률): 0.32
위 내용을 가지고 95%의 신뢰도로 보행자 수는 11명 -> 엥? 너무 많고 비현실적임, 수집된 데이터중 13,14명인 사례는 출퇴근,점심시간 이였으며 10명 이상 건너는 상황은 잘 발견되지 않음, 50%정도만 넘어도 기다릴 가치는 있다고 생각되어 수정
from scipy.stats import nbinom
# 95% 확률 범위의 최대값 계산
max_count_95 = nbinom.ppf(0.95, r, p)
max_count_95
# 11명
# 50% 확률 범위의 최대값 계산
max_count_95 = nbinom.ppf(0.5, r, p)
max_count_95
# 3명누적확률 50% 이상은 3명, 3명 있으면 기다릴 가치가 있다.
6. 회고
- GPT는 GP"F"로 바꿔야함. 앞뒤 서론이 너무 길고 공감 투가 너무 많음. Claude는 코딩능력은 좋은데 필요 이상으로 스켈레톤 코드를 제공해주며, 단순 수식 계산도 틀린 점이 자주 발견됨
- 포아송,음이항 분포 좀 다시 고찰할 필요가 있음. 내 상황에 적절한 분포를 선정하고 데이터를 수집하는게 좋겠다.
- 균등한 데이터 수집을 위해서 하루종일 혹은 대표성을 띄는 시간에 주기적으로 측정하는게 좋겠다.(평소에 부지런하자!)
- Ex) 평일 오전 출근시간 가정 8-9시 집중관찰
본 주제는 매달 한 번씩 호기심을 주제로 분석하는 모임 <월간 데이터 노트>의 결과입니다.
관심이 있으시면 다음 링크를 확인해 보세요!!
'Data Science' 카테고리의 다른 글
| [월데노] 인천 근처에 가면 항구가 가까우니 기름을 넣고 오는게 이득일까? (0) | 2025.05.25 |
|---|---|
| DataScience를 위한 엔지니어링 책 추천 (0) | 2025.05.21 |
| ADP 빅분기 이론과 Python 모듈, 실습코드 정리 - 머신러닝 편 (0) | 2025.04.22 |
| ADP 빅분기 이론과 Python 모듈, 실습코드 정리 - 통계편 (1) | 2025.04.18 |
| 글쓰기 커뮤니티 글또, 참가자부터 운영진까지의 3년 간 회고 (1) | 2025.03.30 |