ADP 빅분기 이론과 Python 모듈, 실습코드 정리

지난번 통계편에 이은 머신러닝문서입니다! 잘못된 내용이나 모호한 내용, 추가되어야하는 내용이 있으면 지적해주세요! 다들 시험에 합격하시길 바라요~

0. 목차

클릭시 해당 컨텐츠로 이동합니다.

https://snowgot.tistory.com/181

ADP 빅분기 이론과 Python 모듈, 실습코드 정리 - 통계편

ADP 시험을 준비하기 위하여 정리했던 방법론과 코드를 저장합니다.빅분기는 범위가 더 좁지만 공통된 부분이 많습니다. 선형계획법이나 기타 내용은 저도 몰라서 못넣었습니다 🤣 잘못된 내용

snowgot.tistory.com

1. 모듈별 디렉토리 정리

ADP 지원 버전: Python 3.7.(공지사항)
ADP 기본제공 Python Package & version

pip install ipykernel=5.1.0
pip install numpy==1.12.6
pip install pandas==1.1.2
pip install scipy==1.7.3
pip install matplotlib==3.0.3
pip install seaborn==0.9.0
pip install statsmodels==0.13.2
pip install scikit-learn==0.23.2
pip install imbalanced-learn==0.5.0

[제34회ADP실기]기본제공_python_package_list.txt

0.01MB

2. 머신러닝 - 지도학습

전체 프로세스
1. 데이터 로딩 및 탐색
2. 결측치 처리
3. 이상치 탐지 및 처리
4. 범주형 변수 인코딩
5. 데이터 스케일링
6. 불균형 데이터 처리
7. 모델링 및 성능 평가

2.1. 결측치 처리 방법

방법	설명	예시
제거	결츷치가 적을 경우	df.dropna()
평균/중앙값 대치	연속형 변수	df['column'].fillna(_mean)
최빈값 대치	범주형 변수	df['column'].fillna(_mode)
KNN Imputer	패턴 반영대체	from sklearn.impute import KNNImputer
Simple Imputer	간단한 대치	from sklearn.impute import SimpleImputer

KNN 대치

from sklearn.impute import KNNImputer
imputer = KNNImputer(n_neighbors= 2)
y = df[['y']]
X = df.drop(columns= 'y')
X_impute = imputer.fit_transform(X)

#fit_transform결과가 ndarray로 나오므로 데이터프레임으로 원복
pd.DataFrame(X_impute, columns = X.columns, index = df.index)

Simple Imputer 대치

import numpy as np
from sklearn.impute import SimpleImputer
imp_mean = SimpleImputer(missing_values=np.nan, strategy='mean')
imp_mean.fit([[7, 2, 3], [4, np.nan, 6], [10, 5, 9]])
SimpleImputer()
X = [[np.nan, 2, 3], [4, np.nan, 6], [10, np.nan, 9]]
print(imp_mean.transform(X))

[[ 7.   2.   3. ]
 [ 4.   3.5  6. ]
 [10.   3.5  9. ]]

2.2. 이상치 처리 방법

기법	설명	예시
IQR 방식	사분위수 기반	Q1 - 1.5IQR, Q3 + 1.5IQR
Z-score	표준정규분포 기반	abs(z) > 3
시각화	boxplot, scatter 사용	sns.boxplot( x= df['col'])

IQR을 이용한 이상치 처리

import numpy as np
# 1. IQR(Interquartile Range) 방법을 이용한 이상치 탐지
def detect_outliers_iqr(df, col):
    Q1 = df[col].quantile(0.25)
    Q3 = df[col].quantile(0.75)
    IQR = Q3 - Q1
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR
    return df[(df[col] < lower_bound) | (df[col] > upper_bound)]

# 각 수치형 변수별 이상치 확인
for col in df_impute_X.columns:
    outliers = detect_outliers_iqr(df_impute_X, col)
    print(f'Column {col} has {len(outliers)} outliers')

# 2. 이상치 처리 방법
# 방법 1: 상한/하한 경계값으로 대체 (Capping)
def treat_outliers_capping(df, col):
    Q1 = df[col].quantile(0.25)
    Q3 = df[col].quantile(0.75)
    IQR = Q3 - Q1
    lower_bound = Q1 - 1.5 * IQR
    upper_bound = Q3 + 1.5 * IQR
    df[col] = np.where(df[col] < lower_bound, lower_bound, df[col])
    df[col] = np.where(df[col] > upper_bound, upper_bound, df[col])
    return df

# 수치형 변수에 대해 이상치 처리
data_cleaned_cap = df_impute_X.copy()
for col in df_impute_X.columns:
    data_cleaned_cap = treat_outliers_capping(data_cleaned_cap, col)

# 방법 2: 이상치가 있는 행 제거 (데이터가 충분할 경우만)
def remove_outliers(df, cols):
    df_clean = df.copy()
    for col in cols:
        Q1 = df[col].quantile(0.25)
        Q3 = df[col].quantile(0.75)
        IQR = Q3 - Q1
        lower_bound = Q1 - 1.5 * IQR
        upper_bound = Q3 + 1.5 * IQR
        df_clean = df_clean[(df_clean[col] >= lower_bound) & (df_clean[col] <= upper_bound)]
    return df_clean

# 중요 변수에 대해서만 이상치 행 제거 (모든 변수에 적용하면 데이터 손실이 클 수 있음)
important_numeric_cols = ['ALB', 'ALP', 'ALT', 'AST', 'BIL', 'CHE', 'CHOL', 'CREA', 'GGT', 'PROT']
data_no_outliers = remove_outliers(df_impute_X, important_numeric_cols)
display(data_no_outliers)

2.3. 범주형 변수인코딩

방법	예시	비고
Label Encoding	순서형 변수	from sklearn.preprocessing import LabelEncoder
One-hot Encoding	명목형 변수	import pd pd.get_dummies()

Label Encoding 방법

from sklearn import preprocessing
le = preprocessing.LabelEncoder()
le.fit([1, 2, 2, 6])
LabelEncoder()
le.classes_
#array([1, 2, 6])
le.transform([1, 1, 2, 6])
#array([0, 0, 1, 2]...)

2.3. 데이터 시각화

sns.heatmap(df.corr(), annot= True, cmap = "YlGnBu" )

2.4. PCA

차원축소기법으로 데이터의 분산을 최대한 보존하면서 고차원이 데이터를 저차원으로 변환
판단 기준
- 분산 설명률: 80~90%의 분산을 설명하는데 필요한 주성분이 원래 특성 수의 절반 이하인가?
- 모델 성능: PCA적용 후 모델 성능이 유지되거나 향상되었는가?
- 다중공선성: 원본 특성간에 높은 상관관계가 많이 존재하는가?
절차
1. 결측치, 이상치 처리, 원-핫 인코딩 사전 진행
2. 스케일링
3. PCA 적용
4. 설명된 분산확인 및 분산비율 시각화
5. 적절한 주성분의 갯수 선택
6. 선택된 주성분의 갯수로 PCA다시 적용
7. 각 주성분이 원래 특성에 얼마나 기여하는지 확인
8. 상위 5개 특성확인

from sklearn.decomposition import PCA
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.preprocessing import StandardScaler

# 데이터는 이미 전처리되었다고 가정 (결측치, 이상치 처리, 원-핫 인코딩 등)
# X는 전처리된 특성 데이터

# 1. 스케일링 (PCA 적용 전 반드시 필요)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

# 2. PCA 적용
pca = PCA()
X_pca = pca.fit_transform(X_scaled)

# 3. 설명된 분산 비율 확인
explained_variance_ratio = pca.explained_variance_ratio_
cumulative_variance_ratio = np.cumsum(explained_variance_ratio)

# 4. 설명된 분산 비율 시각화
plt.figure(figsize=(10, 6))
plt.plot(range(1, len(explained_variance_ratio) + 1), cumulative_variance_ratio, marker='o', linestyle='-')
plt.xlabel('Number of Principal Components')
plt.ylabel('Cumulative Explained Variance Ratio')
plt.title('Explained Variance by Components')
plt.axhline(y=0.8, color='r', linestyle='--', label='80% Variance Threshold')
plt.axhline(y=0.9, color='g', linestyle='--', label='90% Variance Threshold')
plt.legend()
plt.grid(True)
plt.show()

# 5. 적절한 주성분 개수 선택 (예: 80% 분산 유지)
n_components = np.argmax(cumulative_variance_ratio >= 0.8) + 1
print(f"80% 분산을 유지하기 위한 주성분 개수: {n_components}")

# 6. 선택된 주성분 개수로 PCA 다시 적용
pca_selected = PCA(n_components=n_components)
X_pca_selected = pca_selected.fit_transform(X_scaled)

# 7. 각 주성분이 원래 특성에 얼마나 기여하는지 확인
components_df = pd.DataFrame(
    pca_selected.components_,
    columns=X.columns
)

# 8. 각 주성분에 대한 기여도가 높은 상위 5개 특성 확인
for i, component in enumerate(components_df.values):
    sorted_indices = np.argsort(np.abs(component))[::-1]
    top_features = [X.columns[idx] for idx in sorted_indices[:5]]
    top_values = [component[idx] for idx in sorted_indices[:5]]
    print(f"PC{i+1} 주요 특성:")
    for feature, value in zip(top_features, top_values):
        print(f"  {feature}: {value:.4f}")
    print()

# 9. 2D 시각화 (처음 두 개 주성분으로)
plt.figure(figsize=(10, 8))
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=y, cmap='viridis', alpha=0.8)
plt.title('First Two Principal Components')
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.colorbar(label='Target Class')
plt.grid(True)
plt.show()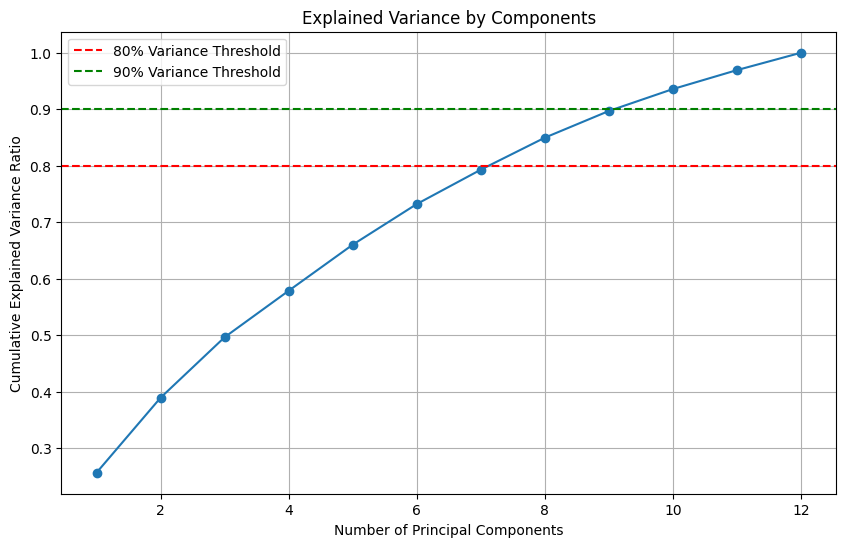

판단근거1: 설명된 분산비율
- 하기의 누적분산 비율이 총 컬럼 12개에서 7개를 담아야지 80%를 설명하므로 차원축소가 효과적이지 않다는 판단 가능

# 누적 설명된 분산 비율을 확인
print("각 주성분별 설명된 분산 비율:")
for i, ratio in enumerate(explained_variance_ratio):
    print(f"PC{i+1}: {ratio:.4f}")

print("\n누적 설명된 분산 비율:")
for i, ratio in enumerate(cumulative_variance_ratio):
    print(f"PC1-PC{i+1}: {ratio:.4f}")
    
    
각 주성분별 설명된 분산 비율:
PC1: 0.2566
PC2: 0.1327
PC3: 0.1071
PC4: 0.0823
PC5: 0.0815
PC6: 0.0719
PC7: 0.0608
PC8: 0.0567
PC9: 0.0472
PC10: 0.0388
PC11: 0.0335
PC12: 0.0308

누적 설명된 분산 비율:
PC1-PC1: 0.2566
PC1-PC2: 0.3893
PC1-PC3: 0.4964
PC1-PC4: 0.5787
PC1-PC5: 0.6602
PC1-PC6: 0.7321
PC1-PC7: 0.7930
PC1-PC8: 0.8497
PC1-PC9: 0.8969
PC1-PC10: 0.9357
PC1-PC11: 0.9692
PC1-PC12: 1.0000

스크리 플롯(Scree Plot)
- Elbow 지점 확인: 대략 4번 지점이 후보군

plt.figure(figsize=(10, 6))
plt.plot(range(1, len(explained_variance_ratio) + 1), explained_variance_ratio, marker='o', linestyle='-')
plt.xlabel('Principal Component')
plt.ylabel('Explained Variance Ratio')
plt.title('Scree Plot')
plt.grid(True)
plt.show()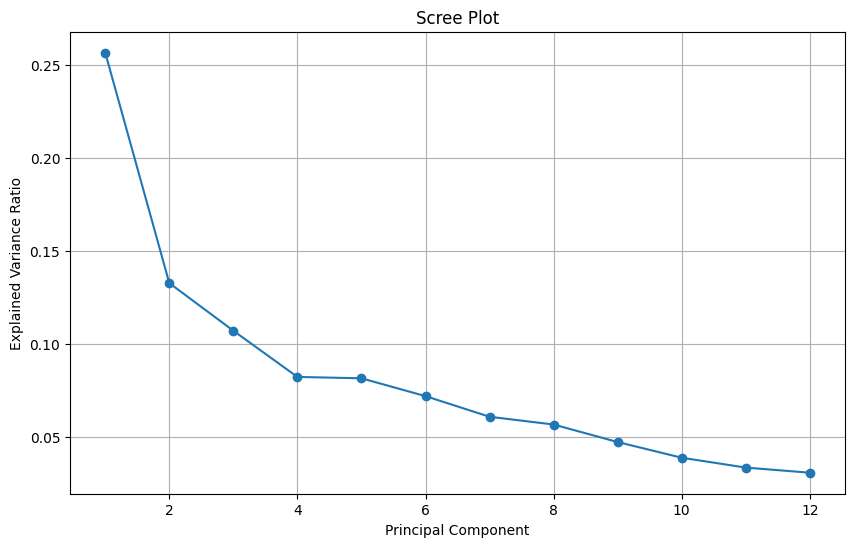

원본데이터와 PCA데이터 성능비교
- cross_val_score의 경우 이진 분류만 가능하기에 다중클래스는 안됨(변환 필요)

from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier

# 원본 스케일링된 데이터에 대한 교차 검증
clf_original = RandomForestClassifier(random_state=42)
scores_original = cross_val_score(clf_original, X_scaled, y, cv=5, scoring='roc_auc')

# PCA 적용 데이터에 대한 교차 검증
clf_pca = RandomForestClassifier(random_state=42)
scores_pca = cross_val_score(clf_pca, X_pca_selected, y, cv=5, scoring='roc_auc')

print(f"원본 데이터 평균 ROC-AUC: {scores_original.mean():.4f} (±{scores_original.std():.4f})")
print(f"PCA 데이터 평균 ROC-AUC: {scores_pca.mean():.4f} (±{scores_pca.std():.4f})")

다중공선성 검사
- 특성간 높은 상관관계 발견(0.7 이상) 되면 PCA가 유용할 수 있음
- 해당 높은 특성들은 독립적인 주성분으로 변환

from sklearn.preprocessing import StandardScaler
from scipy.stats import spearmanr
import seaborn as sns

# 상관관계 행렬 계산
correlation_matrix = X.corr()

# 상관관계 히트맵 표시
plt.figure(figsize=(12, 10))
sns.heatmap(correlation_matrix, annot=False, cmap='coolwarm', center=0)
plt.title('Feature Correlation Matrix')
plt.tight_layout()
plt.show()

# 높은 상관관계(0.7 이상)를 가진 특성 쌍 찾기
high_corr_pairs = []
for i in range(len(correlation_matrix.columns)):
    for j in range(i+1, len(correlation_matrix.columns)):
        if abs(correlation_matrix.iloc[i, j]) > 0.7:
            high_corr_pairs.append((correlation_matrix.columns[i], correlation_matrix.columns[j], correlation_matrix.iloc[i, j]))

print("높은 상관관계를 가진 특성 쌍:")
for pair in high_corr_pairs:
    print(f"{pair[0]} - {pair[1]}: {pair[2]:.4f}")

2.3. 스케일링

방법	설명	특장점
Standard Scaler(정규화)	각 데이터에 평균을 뺴고 표준편차 나누기 (x - x_bar / x_std)	이상치, 분포가 skewed되어있을때
MinMax Scaler(표준화)	데이터를 0과 1사이로 조정 ( x- x_min / x_max - x_min)	이상치에 영향을 많이 받음
Robust Scaler	중앙 값과 IQR를 이용해 조정 (x - median / IQR)	이상치에 덜 민감

정규화 스케일링

from sklearn.preprocessing import StandardScaler
data = [[0, 0], [0, 0], [1, 1], [1, 1]]
scaler = StandardScaler()
print(scaler.fit(data))
StandardScaler()
print(scaler.mean_)
#[0.5 0.5]
print(scaler.transform(data))
#[[-1. -1.]
# [-1. -1.]
# [ 1.  1.]
# [ 1.  1.]]

2.4. 데이터 샘플링

방법	설명	사용법
언더샘플링	다수 클래스 줄임	from imblearn.under_sampling import RandomUnderSampler SMOTE 클래스 대신 사용하면 됨
오버샘플링	소수 클래수 복제	SMOTE
클래스 가중치	모델이 직접 적용, 데이터가 작아 오버샘플링이 부담스러울 때	class_weight = 'balanced' (Logistic, RF, SVC, GBC 등 지원)

SMOTE 코드

from imblearn.over_sampling import SMOTE

X = df.drop(columns=['Category', 'target'])
y = df['target']
smote = SMOTE(random_state = 42)
X_resampled, y_resampled = smote.fit_resample(X, y)

2.4. 평가지표 metrics

메트릭	설명	사용시점
Precision	Positive 예측 한 것 중 실제 Positive	FP가 중요한 문제(스팸 필터처럼 잘못 걸러내면 안됄 때)
Recall(Sensitivity)	실제 Positive중 Positive로 예측한 비율	FN가 중요힌 문제(암 진단처럼 놓지면 안될 때)
F1-score	Precision과 Recall의 조화 평균	둘 다 중요할 때
AUC-ROC	다양한 threshhold에서 TPR vs FPR 곡선의 아래 면적	전체적인 분류 성능이 중요할 때
PR-AUC	Precision vs Recall 곡선의 면적	불균형이 매우 심하여 Positive가 극소수 일때

메트릭 코드 모음

# 분류모델
from sklearn.metrics import accuracy_score, precision_score,recall_score
from sklearn.metrics import f1_score, confusion_matrix, roc_auc_score, classification_report
# 회귀모델
from sklearn.metrics import mean_squared_error, mean_absolute_error
from sklearn.metrics import r2_score, adjusted_rand_score

# 비지도학습 군집
from sklearn.metrics import silhouette_score

classification_report 읽기
- support: 해당 클래스의 샘플 수
- macro avg: 일반적인 지표
- weight avg: 샘플수 가중치를 더한 지표

ROC Curve

import matplotlib.pyplot as plt
from sklearn.metrics import roc_curve, roc_auc_score

# 모델 학습 (예시)
model = RandomForestClassifier(random_state=42)
model.fit(X_train, y_train)

# 테스트 데이터에 대한 예측 확률
y_pred_proba = model.predict_proba(X_test)[:, 1]  # 양성 클래스(1)에 대한 확률

# ROC 커브 계산
fpr, tpr, thresholds = roc_curve(y_test, y_pred_proba)

# AUC 계산
roc_auc = roc_auc_score(y_test, y_pred_proba)

# ROC 커브 그리기
plt.figure()
plt.plot(fpr, tpr, color='blue', label=f'ROC curve (AUC = {roc_auc:.2f})')
plt.plot([0, 1], [0, 1], color='gray', linestyle='--')  # 대각선 기준선
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()

2.5. 머신러닝 스켈레톤 코드 - 분류

from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import RandomForestClassifier
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split

X = df.drop(columns = ['Kwh8','date','datetime'])
y = df['Kwh8']

X_train, X_test, y_train, y_test = train_test_split(X,y, random_state= 42, stratify= y, test_size= 0.2)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

# 모델 리스트와 이름
models = [
	('Logistic', LogisticRegression(solver='liblinear')), #sklearn 0.23. 에러 대응
    ('RandomForest', RandomForestClassifier(random_state=42)),
    ('SVM', SVC(random_state=42))
]

# 모델 학습 및 평가
for model_name, model in models:
    model.fit(X_train, y_train)
    
    # 예측 수행
    y_pred_train = model.predict(X_train)
    y_pred_test = model.predict(X_test)
    
    # 성능 평가 (train)
    print(f'Train - {model_name} Model')
    print(classification_report(y_train, y_pred_train))
    
    # 성능 평가 (test)
    print(f'Test - {model_name} Model')
    print(classification_report(y_test, y_pred_test))

2.5. 머신러닝 스켈레톤 코드 - 분류(cv)

from sklearn.metrics import classification_report, accuracy_score
from sklearn.model_selection import cross_val_score, KFold, StratifiedKFold

# 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42, stratify=y, test_size=0.3)
print(X_train.shape, X_test.shape, y_train.shape, y_test.shape)

# 교차 검증 설정
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=42)

# 모델 리스트와 이름
models = [
    ('Logistic', LogisticRegression(solver='liblinear')), #sklearn 0.23. 에러 대응
    ('RandomForest', RandomForestClassifier(random_state=42)),
    ('SVM', SVC(random_state=42))
]

# 모델 학습 및 평가
for model_name, model in models:
    # 교차 검증 수행
    cv_scores = cross_val_score(model, X_train, y_train, cv=cv, scoring='accuracy')
    print(f'\n{model_name} Cross-Validation:')
    print(f'CV Scores: {cv_scores}')
    print(f'Mean CV Score: {cv_scores.mean():.4f} ± {cv_scores.std():.4f}')
    
    # 전체 훈련 데이터로 모델 학습
    model.fit(X_train, y_train)
    
    # 예측 수행
    y_pred_train = model.predict(X_train)
    y_pred_test = model.predict(X_test)
    
    # 성능 평가 (train)
    print(f'\nTrain - {model_name} Model')
    print(classification_report(y_train, y_pred_train))
    
    # 성능 평가 (test)
    print(f'\nTest - {model_name} Model')
    print(classification_report(y_test, y_pred_test))
    
    print('-' * 70)

# 다양한 교차 검증 방법 비교 (선택적)
print("\n다양한 교차 검증 방법 비교 (RandomForest 모델):")
cv_methods = {
    'KFold (k=5)': KFold(n_splits=5, shuffle=True, random_state=42),
    'StratifiedKFold (k=5)': StratifiedKFold(n_splits=5, shuffle=True, random_state=42),
    'StratifiedKFold (k=10)': StratifiedKFold(n_splits=10, shuffle=True, random_state=42)
}

rf_model = RandomForestClassifier(random_state=42)
for cv_name, cv_method in cv_methods.items():
    cv_scores = cross_val_score(rf_model, X_train, y_train, cv=cv_method, scoring='accuracy')
    print(f'{cv_name}: {cv_scores.mean():.4f} ± {cv_scores.std():.4f}')

2.6. 종속변수에 영향 해석하기

로지스틱 회귀 베타계수 추정
- 양수는 변수가 증가감에 따라 간염 화률의 증가, 음수는 감소
- 로즈오즈 해석: 계수가 0.5이면 1단위 증가할 때 간염 발생 로그오즈 0.05 증가
- 오즈비 해석: exp(계수)값으로 계산하며 1.5이면 변수 1단위 증가할 때 간염 발생 오즈 50% 증가 0.8이면 20% 감소, 1이면 영향 미치지 않음

# 로지스틱 회귀 모델 학습
log_model = LogisticRegression(solver='liblinear')
log_model.fit(X_train, y_train)

# 계수 및 변수명 가져오기
coefficients = log_model.coef_[0]
feature_names = X.columns

# 계수 크기순으로 정렬하여 출력
coef_df = pd.DataFrame({'Feature': feature_names, 'Coefficient': coefficients})
coef_df = coef_df.sort_values('Coefficient', ascending=False)
print("로지스틱 회귀 계수 (양수=간염 위험 증가, 음수=간염 위험 감소):")
print(coef_df)

# 오즈비(Odds Ratio) 계산 - 해석이 더 직관적임
coef_df['Odds_Ratio'] = np.exp(coef_df['Coefficient'])
print("\n오즈비 (1보다 크면 위험 증가, 1보다 작으면 위험 감소):")
print(coef_df[['Feature', 'Odds_Ratio']])

Feature Importance

# Random Forest 모델 학습
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train)

# 특성 중요도 추출 및 시각화
importances = rf_model.feature_importances_
indices = np.argsort(importances)[::-1]

feature_importance_df = pd.DataFrame({
    'Feature': feature_names[indices],
    'Importance': importances[indices]
})

plt.figure(figsize=(10, 6))
sns.barplot(x='Importance', y='Feature', data=feature_importance_df[:10])
plt.title('Top 10 Important Features for Hepatitis Prediction (Random Forest)')
plt.tight_layout()
plt.show()

SHAP value
- 게임 이론이 기반, 각 특성이 모델 예측에 미치는 기여도를 배분
- 양수면 해당 특성이 예측 확률을 증가시키는 방향으로 기여, 음수는 감소시키는 방향으로 기여
- 개별 예측 분석, 상호작용 효과 파악, 모든 모델에 적용할 수 있는 장점

#!pip install shap
import shap

# SHAP 값 계산 (예: Random Forest 모델)
explainer = shap.TreeExplainer(rf_model)
shap_values = explainer.shap_values(X_test)

# SHAP 값 요약 시각화
shap.summary_plot(shap_values, X_test, feature_names=feature_names)

2.6. tensorflow 1.13.1 기준 지도학습 코드

import tensorflow as tf
import numpy as np
import os

# TensorFlow 1.x 환경에서 Eager Execution을 비활성화
tf.compat.v1.disable_eager_execution()

# 데이터 생성 (이진 분류용)
X_data = np.random.rand(100, 2)  # 100개의 샘플, 2개의 특성
y_data = np.random.randint(2, size=(100, 1))  # 100개의 이진 타겟 값 (0 또는 1)

# 모델 정의 (Sequential API)
model = tf.keras.models.Sequential()
model.add(tf.keras.layers.Dense(10, input_dim=2, activation='relu'))  # 은닉층
model.add(tf.keras.layers.Dense(1, activation='sigmoid'))  # 이진 분류를 위한 sigmoid 출력층

# 모델 컴파일
model.compile(optimizer='adam', loss='binary_crossentropy', metrics=['accuracy'])

# 체크포인트 설정
checkpoint_path = "training_checkpoints/cp.ckpt"
checkpoint_dir = os.path.dirname(checkpoint_path)

# 체크포인트 콜백 설정
cp_callback = tf.keras.callbacks.ModelCheckpoint(filepath=checkpoint_path,
                                                 save_weights_only=True,
                                                 verbose=1)
# 모델 학습 (체크포인트 콜백 적용)
model.fit(X_data, y_data, epochs=10, batch_size=10, callbacks=[cp_callback])
# 모델 저장 (전체 모델 저장)
model.save('saved_model/my_model')
# 모델 불러오기
new_model = tf.keras.models.load_model('saved_model/my_model')
# 불러온 모델 평가
loss, accuracy = new_model.evaluate(X_data, y_data)
print(f"불러온 모델 정확도: {accuracy:.4f}")
# 체크포인트에서 가중치만 불러오기
new_model.load_weights(checkpoint_path)
# 불러온 체크포인트의 가중치로 다시 평가
loss, accuracy = new_model.evaluate(X_data, y_data)
print(f"체크포인트에서 불러온 모델 정확도: {accuracy:.4f}")
# 분류 예측
predictions = new_model.predict(X_data)
print(f"예측값 (0 또는 1로 변환): \n{(predictions > 0.5).astype(int)}")

3. 머신러닝 - 비지도학습

3.1. Kmeans

import pandas as pd
from sklearn.cluster import KMeans

# KMeans 설정 및 클러스터링 수행
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(data)

# 클러스터 결과를 데이터프레임에 추가
data['cluster'] = kmeans.labels_

# 결과 확인
print(data.head())

3.2. DBSCAN

import pandas as pd
from sklearn.cluster import DBSCAN

# DBSCAN 설정 및 클러스터링 수행
dbscan = DBSCAN(eps=0.5, min_samples=5)
dbscan.fit(data)

# 클러스터 결과를 데이터프레임에 추가
data['cluster'] = dbscan.labels_

# 결과 확인
print(data.head())

3.3. Elbow method

# 클러스터 수에 따른 inertia (군집 내 거리 합) 계산
inertia = []
K = range(1, 11)  # 1~10개의 클러스터를 테스트
for k in K:
    kmeans = KMeans(n_clusters=k, random_state=42)
    kmeans.fit(data)
    inertia.append(kmeans.inertia_)

# Elbow Method 그래프 시각화
plt.figure(figsize=(8, 6))
plt.plot(K, inertia, 'bx-')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Inertia')
plt.title('Elbow Method For Optimal k')
plt.show()

3.4. 실루엣 계수

from sklearn.metrics import silhouette_score

# 실루엣 계수를 저장할 리스트
silhouette_avg = []

# 2~10개의 클러스터를 테스트
K = range(2, 11)
for k in K:
    kmeans = KMeans(n_clusters=k, random_state=42)
    labels = kmeans.fit_predict(data)
    silhouette_avg.append(silhouette_score(data, labels))

# 실루엣 계수 시각화
plt.figure(figsize=(8, 6))
plt.plot(K, silhouette_avg, 'bx-')
plt.xlabel('Number of clusters (k)')
plt.ylabel('Silhouette Score')
plt.title('Silhouette Score For Optimal k')
plt.show()

4. 생존 분석

생존분석 정리글입니다.

https://snowgot.tistory.com/137

생존분석과 lifeline 패키지 활용 - LogRank, 카플란-마이어, 콕스비례위험모형

1. 생존분석이란시간-이벤트 데이터(예: 생존 시간, 고장 시간 등)를 분석하는 데 사용됨주요 목표는 생존 시간 분포를 추정하고, 생존 시간에 영향을 미치는 요인을 식별하며, 여러 그룹 간의 생

snowgot.tistory.com

4.1. 생존 분석 분류

생존 분석: 다양한 모델링 기법을 포함하는 광범위한 분야로, 시간-이벤트 데이터를 분석
- 카플란-마이어 추정법: 특정 시간까지 이벤트가 발생하지 않을 확률을 추정하는 방법입니다. 사건이 독립적이라는 가정
- Log-Rank 테스트: 두 그룹 간의 시간에 따른 생존율 차이를 검정
- 콕스 비례 위험 모형: 시간에 따른 위험을 모델링하며, 공변량이 시간에 따라 비례적으로 위험률에 영향을 미친다는 가정을 기반

4.2. 카플란 마이어

특정 시간까지 이벤트가 발생하지 않을 확률(생존 함수)을 비모수적으로 추정하는 방법
각 시간 점에서 생존 확률을 계산하고, 이를 통해 전체 생존 곡선을 작성.
사건이 독립적이라는 가정이 있지만, 실제로는 이 가정이 항상 만족되지 않을 수 있음(실제로 병은 누적되는 대미지가 있으므로)
$\hat{S}(t) = \prod_{t_i \leq t} \left(1 - \frac{d_i}{n_i}\right)$

import pandas as pd
import matplotlib.pyplot as plt
from lifelines import KaplanMeierFitter

# 예시 데이터 생성
data = {
    'duration': [5, 6, 6, 7, 8, 8, 10, 12, 14, 15, 18, 20, 25],
    'event': [1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1]
}

df = pd.DataFrame(data)

# Kaplan-Meier Fitter 생성
kmf = KaplanMeierFitter()

# 생존 함수 적합
kmf.fit(durations=df['duration'], event_observed=df['event'])

# 생존 곡선 시각화
plt.figure(figsize=(10, 6))
kmf.plot_survival_function()
plt.title('Kaplan-Meier Survival Curve')
plt.xlabel('Time')
plt.ylabel('Survival Probability')
plt.grid(True)
plt.show()

4.3. Log-Rank

카플란 마이어 기법의 응용
두 그룹 간의 시간에 따른 생존율 차이를 검정하는 방법
각 시간 점에서 관찰된 사건 수와 기대 사건 수를 비교하여(카이제곱검정), 두 그룹의 생존 곡선이 통계적으로 유의미하게 다른지를 평가
$\chi^2 = \frac{(O_1 - E_1)^2}{V_1} + \frac{(O_2 - E_2)^2}{V_2}$

import pandas as pd
from lifelines import KaplanMeierFitter
from lifelines.statistics import logrank_test

# 데이터 생성
data = {
    'group': ['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B'],
    'duration': [6, 7, 10, 15, 23, 5, 8, 12, 18, 22],
    'event': [1, 0, 1, 0, 1, 1, 1, 0, 1, 1]
}

df = pd.DataFrame(data)

# 두 그룹 나누기
groupA = df[df['group'] == 'A']
groupB = df[df['group'] == 'B']

# Kaplan-Meier Fitter 생성
kmf_A = KaplanMeierFitter()
kmf_B = KaplanMeierFitter()

# 생존 함수 적합
kmf_A.fit(durations=groupA['duration'], event_observed=groupA['event'], label='Group A')
kmf_B.fit(durations=groupB['duration'], event_observed=groupB['event'], label='Group B')

# Log-Rank 테스트 수행
results = logrank_test(groupA['duration'], groupB['duration'], event_observed_A=groupA['event'], event_observed_B=groupB['event'])
results.print_summary()

시각화 코드

import pandas as pd
import matplotlib.pyplot as plt
from lifelines import KaplanMeierFitter

# 데이터 생성
data = {
    'group': ['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B'],
    'duration': [6, 7, 10, 15, 23, 5, 8, 12, 18, 22],
    'event': [1, 0, 1, 0, 1, 1, 1, 0, 1, 1]
}

df = pd.DataFrame(data)

# 두 그룹 나누기
groupA = df[df['group'] == 'A']
groupB = df[df['group'] == 'B']

# Kaplan-Meier Fitter 생성
kmf_A = KaplanMeierFitter()
kmf_B = KaplanMeierFitter()

# 생존 함수 적합
kmf_A.fit(durations=groupA['duration'], event_observed=groupA['event'], label='Group A')
kmf_B.fit(durations=groupB['duration'], event_observed=groupB['event'], label='Group B')

# 생존 곡선 시각화
plt.figure(figsize=(10, 6))
kmf_A.plot_survival_function()
kmf_B.plot_survival_function()
plt.title('Kaplan-Meier Survival Curves')
plt.xlabel('Time (months)')
plt.ylabel('Survival Probability')
plt.legend()
plt.grid(True)
plt.show()

4.4. 콕스비레 위험모형

카플란마이어 추정법은 사건이 독립적이라는 가정의 한계 따라서 시간에 따른 사건 발생 위험률(위험 함수)을 모델링
공변량(독립변수)이 시간에 따라 비례적으로 위험률에 영향을 미친다는 가정
기준 위험률와 공변량의 선형 결합을 지수 함수 형태로 결합하여 위험률을 표현
- 기준위험률(λ0(t)): 시간 t 기준 위험률로 공변량의 영향을 제거한 상태의 기본적인 위험률
- 공변량(Covariates, X): 사건 발생에 영향을 미칠 수 있는 변수들
시간-의존적 위험률을 모델링할 수 있으며, 공변량이 생존 시간에 미치는 영향을 평가하는 데 유용
$\lambda(t \mid X) = \lambda_0(t) \exp(\beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p)$

import pandas as pd
from lifelines import CoxPHFitter
import matplotlib.pyplot as plt

# 예시 데이터 생성
```
duration: 환자가 생존한 기간(개월 수)
event: 사건 발생 여부(1 = 사망, 0 = 생존)
age: 환자의 나이
treatment: 치료 방법(0 = 치료 A, 1 = 치료 B)
```
data = {
    'duration': [5, 6, 6, 7, 8, 8, 10, 12, 14, 15, 18, 20, 25, 5, 7, 12, 13, 14, 16, 20],
    'event': [1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1],
    'age': [50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 55, 60, 65, 70, 75, 80, 85],
    'treatment': [0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1]
}

df = pd.DataFrame(data)

# 콕스 비례 위험 모형 적합
cph = CoxPHFitter()
cph.fit(df, duration_col='duration', event_col='event')

# 모형 요약 출력
cph.print_summary()

# 생존 곡선 시각화
cph.plot()
plt.title('Hazard Ratios')
plt.show()

'Data Science' 카테고리의 다른 글

DataScience를 위한 엔지니어링 책 추천 (0)	2025.05.21
🚥 횡단보도에 몇 명이 있어야 금방 신호가 파란색을 바뀔까? (0)	2025.04.26
ADP 빅분기 이론과 Python 모듈, 실습코드 정리 - 통계편 (0)	2025.04.18
글쓰기 커뮤니티 글또, 참가자부터 운영진까지의 3년 간 회고 (1)	2025.03.30
왜 프로덕트 팀은 A/B테스트를 사랑할까? (feat 인과추론) (1)	2025.01.18

지지플랏의 DataScience

ADP 빅분기 이론과 Python 모듈, 실습코드 정리 - 머신러닝 편

0. 목차

1. 모듈별 디렉토리 정리

2. 머신러닝 - 지도학습

2.1. 결측치 처리 방법

2.2. 이상치 처리 방법

2.3. 범주형 변수인코딩

2.3. 데이터 시각화

2.4. PCA

2.3. 스케일링

2.4. 데이터 샘플링

2.4. 평가지표 metrics

2.5. 머신러닝 스켈레톤 코드 - 분류

2.5. 머신러닝 스켈레톤 코드 - 분류(cv)

2.6. 종속변수에 영향 해석하기

2.6. tensorflow 1.13.1 기준 지도학습 코드

3. 머신러닝 - 비지도학습

3.1. Kmeans

3.2. DBSCAN

3.3. Elbow method

3.4. 실루엣 계수

4. 생존 분석

4.1. 생존 분석 분류

4.2. 카플란 마이어

4.3. Log-Rank

4.4. 콕스비레 위험모형

'Data Science' 카테고리의 다른 글

티스토리툴바

ADP 빅분기 이론과 Python 모듈, 실습코드 정리 - 머신러닝 편

0. 목차

1. 모듈별 디렉토리 정리

2. 머신러닝 - 지도학습

2.1. 결측치 처리 방법

2.2. 이상치 처리 방법

2.3. 범주형 변수인코딩

2.3. 데이터 시각화

2.4. PCA

2.3. 스케일링

2.4. 데이터 샘플링

2.4. 평가지표 metrics

2.5. 머신러닝 스켈레톤 코드 - 분류

2.5. 머신러닝 스켈레톤 코드 - 분류(cv)

2.6. 종속변수에 영향 해석하기

2.6. tensorflow 1.13.1 기준 지도학습 코드

3. 머신러닝 - 비지도학습

3.1. Kmeans

3.2. DBSCAN

3.3. Elbow method

3.4. 실루엣 계수

4. 생존 분석

4.1. 생존 분석 분류

4.2. 카플란 마이어

4.3. Log-Rank

4.4. 콕스비레 위험모형

'Data Science' 카테고리의 다른 글

관련글

티스토리툴바