1. 목차
- 5.1. 나이브베이즈(NB)
- 5.2. 선형판별분석(LDA)
2. 본문
들어가기에 앞서 이책이 이론적으로는 확실히 친절한 책은 아님을 다시 확인시켜주는 단원이라 생각된다. 특히 나이브 베이즈와 판별분석은 그렇게 와닿는 예시는 아니니 다른 타 도서나 추가 공부가 필요함을 미리 알아두자.
2.1. 나이브베이즈(NB)
2.1.1. 베이즈 추정
추론 대상의 사전확률과 정보를 가지고 사후 확률을 추론하는 통계 기법을 베이즈 추정(Bayesian Estimation)이라고 한다.

- $ P(\theta | X) $: 데이터 $X$가 주어졌을 때 모수 $\theta$의 사후 확률 분포(posterior distribution)
- $ P(X | \theta) $: 모수 $\theta$ 가 주어졌을 때 데이터 $X$의 우도(likelihood)
- $ P(\theta) $: 데이터 $\theta$의 사전 확률 분포(prior distribution)
- $ P(X) $: 데이터 X의 주어진 확률
쉽게 말하면 기계의 성능을 평가할 때 부품 몇개를 무작위로 뽑아서 테스트 해볼 수도 있지만, 기계의 과거 성능 검사 기록이나 부품의 성능 자료를 얻을 수 도 있다.
- 예시
- 1. 사전확률
- $P(C)$: 암환자일 확률 = 0.105
- $P(~C)$: 암환자가 아닐 확률 = 0.895
- 2. 조건부확률
- 1. 사전확률
| 암환자(C) | 암 환자 아님(~C) | |
| Positive(양성) | $ P( Positive | C) $= 0.905 | $P( Positive | \sim C)$ = 0.204 |
| Negative(음성) | $ P( Negative | C) $ = 0.095 | $P( Negative | \sim C)$ = 0.796 |
위 예시에서 어떤사람이 양성(P)일 때, 이사람이 암환자일 확률 구해보자. 다음과 같은 식으로 표현된다.
$P(C | Positive)$ = $\frac{P(Positive|C)*P(C)}{P(Positive)} $
이 때 $P(Positive)$는 암 환자이면서 양성 판정을 받을 확률 $P(Positive, C)$와 암환자가 아닌데 양성판정을 받을 확률의 합$P(Positive, \sim C)$의 합과 같다.
$P(Positive)$ = $P(Positive | C) * P(C) + P(Positive | \sim C)*P(\sim C)$
따라서 $P(C|Positive)$ 는 0.905*0.105 / (0.905*0.105 + 0.204*0.895) = 0.342 가 된다.
2.1.2. 그래서 베이즈분류란?
베이즈 분류는 주어진 클래스에 대한 모든 특징들이 서로 독립적이라는 가정하에 이루어지는 방법론이다. 따라서 $P(X|C)$는 다음과 같이 분해 된다.
$P(X|C) = P(x_{1} + x_{2}, .... x_{n} | C ) = P(x_{1} | C) * P(x_{2} | C) ... P(X_{n} | C)$
- 학습
- 각 클래스 $C$의 사전 확률 $P(C)$를 추정
- 각 클래스 $C$에 대해 주어진 클래스에서 각 특징 $x_{i}$의 조건의 확률 $P(x_{i}|C)를 추정
- 예측
- 새로운 데이터 포인트 X가 주어졌을 때, 각 클래스 C에 대해서 사후 확률 $P(C|X)$를 계산
- 사후 확률 $P(C|X)$가 가장 큰 클래스를 선택하여 예측
나이브베이즈의 장점은 간단하고 구현하고 용이하며 계산이 빠르다. 또한 데이터가 적어도 잘 작동하며 다수의 특징(feature)를 다룰 수 있다는 것이다. 반면 조건부 독립성 가정이 실제 데이터에서는 성립 할 수 않을 수 있다. 그 밖에도 활용범위로 텍스트 분류, 스팸 필터링, 감정 분석에 널리 사용된다.
2.2. 선형판별분석(LDA)
선형판별분석(Linear Discriminant Analysis, 이하 LDA)는 이름에 걸맞게 가상의 선형에 사영(projection)하여 분류할 수 있는 직선을 찾는 것을 목표로 하는 방법입니다. 분류의 카테고리에 들어가지만 고차원의 데이터 세트를 저차원에 투영하여 차원축소를 한다는 점에서는 PCA와 같이 언급되는 경우가 많습니다만 PCA는 가장 변동성이 큰 축을 찾지만 LDA는 입력 데이터의 결정 값을 최대한으로 분리 할 수 있는 축을 찾는 다는 점이 특징이 있습니다. 또한 PCA는 비지도학습 LDA는 지도학습이라는 큰 차이점 도 있습니다.

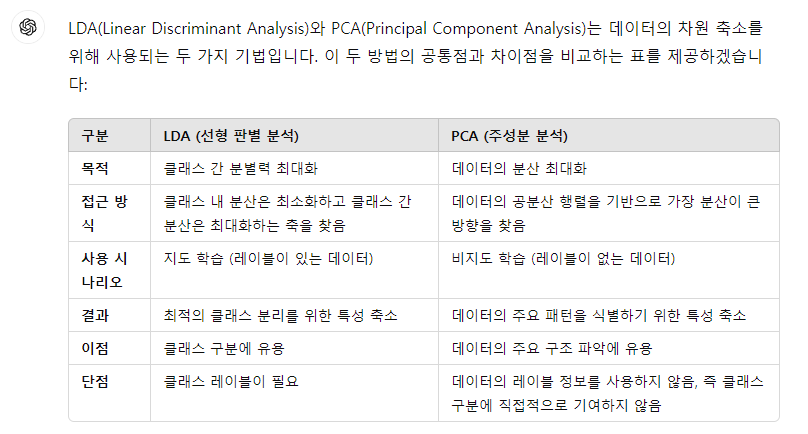
LDA는 특정 공간상에서 클래스 분리를 최대화하는 축을 찾기 위해서 클래스 간 분산(between class scatter)과 클래스 내부분산(with in class scatter)의 비율을 최대화 하는 방식으로 차원을 축소한다. 방법을 파헤치기 전에 선형대수에서 중요한 고유벡터와 고유값이라는 개념을 이해하고 가자
2.2.1. 고유값과 고유벡터
- 원래 행렬이란 기존의 벡터값을 "선형변환"을 하는 기하학적 의미를 가지고 있다.
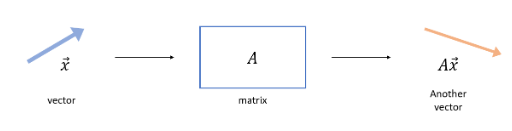
- 예컨데 [1,1]이라는 벡터(파란색)에 행렬을 곱해주면 변환된 벡터(빨간색)처럼 방향이 바뀐다.

- 그렇다면 모든 행렬은 기존 벡터(파란색)의 방향을 바꾸는가? 는 또 아닐 것이 방향을 그대로하되 크기만 변하게 하는 행렬 역시 존재한다는 것이 합리적인 생각이다. 마치 벡터의 방향을 그대로 키우거나 줄이는 것처럼 말이다.

- 이는 선형변환이기도 하지만 기존 벡터에 상수배를 곱한 것과 같은 원리이다. 이때 [1,1] 그러니까 $\overrightarrow{x}$로 표현하고 이를 고유 벡터, 해당하는 상수배 숫자 $\lambda$를 고유값이라고 한다.
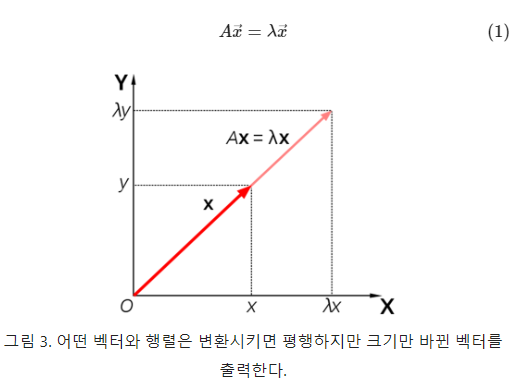
- 기하학적 의미로 정리하자면 고유벡터는 행렬(선형변환)에 의해 방향은 보존되고 그 크기(스케일)만 변화하는 방향벡터를 뜻한다. 고유값은 고유 벡터에 의하여 변하는 정도를 나타내는 값이라 할 수 있다.
위 내용의 디테일은 공돌이의 수학정리 노트 - 고윳값과 고유벡터 에서 찾아볼 수 있다.
2.2.2. LDA의 작동순서
1. 클래스 내부와 클래스 간 차이를 구하기
- 클래스 내에서 데이터가 얼마나 흩어져있는지(분산), 그리고 클래스들이 서로 얼마나 떨어져있는지(분간 차이)를 각각 정리
- 클래스 내 분산행렬($S_{W}$): 각 클래스 내에서 데이터포인트와 해당 클래스 평균의 차이를 측정
- 클래스 간 분산행렬($S_{B}$): 각 클래스의 평균이 전체 데이터의 평균에서 얼마나 떨어져 있는지 측정
LDA는 $\frac{ S_{B} }{ S_{W} }$를 최대화하기 위한 방향으로 설정합니다. 다시 말해 해당하는 클래스 내 분산 ($S_{W}$) 을 최소화하는 반면 클래스 간 분산 ($S_{B}$) 을 최대화하기 위한 방향입니다. 그래야 두 클래스를 구분하기 쉬워질 테니까요! 여기서 최대화, 최소화를 하는 목적어는 데이터이며 데이터의 흩어진 정도를 조절하는 것입니다.
위 $\frac{ S_{B} }{ S_{W} }$식을 최대화 하기 위한 방법론으로 고유값을 이용할 수 있습니다.
- 클래스 A,B가 있고 각 데이터가 3개가 있을때의 계산을 진행해보겠습니다.

- $S_{W}$ 계산 방법

- $S_{B}$ 계산방법

2. 행렬분해
- $S_{W}$, $S_{B}$ 라고 하면 다음 식으로 두 행렬을 고유벡터로 분해
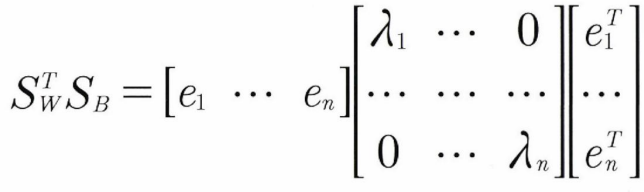
- 우측식은 $ E\lambda E^{T} $와 같은 형태로 분해된 것이다. $E$는 각 고유 벡터를 열로 갖는 행렬이며, $\lambda$ 는 대각선상에 고유값을 가지고 나머지 원소는 모두 0인 대각 행렬이 생성
- 고유 벡터는 클래스를 구분한느 유리한 방향을 나타내며, 고유값은 그 방향의 중요도를 표현하는 것. 고유값이 클수록 더 클래스간의 분리가 잘 일어나는 방향.
3. 고유값이 가장 큰 순서대로 K개 만큼 추출, 고유벡터를 이용해 새롭게 입력 데이터를 변환
- 고유값이 큰 고유벡터를 선택하여 저차원 공간으로 투영
2.2.3. 선형판별분석의 현대 활용
원리를 보면 간단하고 파워풀한 분류방법으로보이나 몇가지 한계로 인해 현재는 다른 머신러닝모델에 비해 두각되지 않는 는 특징이있다. 선형판별분석은 데이터가 선형적으로 구분 가능하다는 선형성 가정, 데이터가 정규분포를 따른다는 정규성 가정, 모든 클래스가 동일한 공분산을 가진다는 동일 공분산 가정 등 가정이 많아 제한적으로 쓰일 수 밖에 없는 특징을 가지고 있다.
또한 데이터의 차원이 높은 경우 $S_{W}$ 분산 내 행렬을 계산하는데 리소스 소모가 많이 되며 특이 행렬이 되어 역행렬을 계산할 수 없을 때 사용할 수 없다. 이러한 제한점 때문에 SVM, 트리기반 모델, 딥러닝 모델에 밀려 자주 쓰이지 않는 한계를 가지고 있다.
'Data Science > 데이터과학을 위한 통계' 카테고리의 다른 글
| (11) DSforS : Chap5 5.5 불균형 데이터 다루기 (0) | 2024.06.16 |
|---|---|
| (10) DSforS : Chap5. 분류 5.3 ~ 5.4. 로지스틱회귀(LoR), 분류모델 평가 (0) | 2024.06.11 |
| (8) DSforS : Chap4. 회귀와 예측 4.5 ~ 4.8 회귀방정식의 해석 ~ 끝 (0) | 2024.06.04 |
| (7) DSforS : Chap 4. 회귀와 예측 4.1 ~ 4.4 단순선형회귀 ~ 요인변수 (1) | 2024.06.03 |
| (6) DSforS : Chap 3 통계적 실험과 유의성 검정 3.4 ~ 3.8. (0) | 2024.05.27 |