| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 공유경제
- 풀러스
- 평창
- CC#3
- 데이터
- 정형데이터
- 토스트마스터
- 사이허브
- PGTM
- 데이터분석
- 영화
- publicspeaking
- 임상통계
- Toastmaster
- 영어연설
- 카이제곱분포
- 제약
- 2018계획
- 취업
- SQLD
- CC#5
- 데분
- Public Speaking
- 구글#빅쿼리#데이터분석
- 연설
- 엘뱌키안
- 대중연설
- F분포
- 분석
- 인과추론
- Today
- Total
지지플랏의 DataScience
신뢰구간의 2가지 계산방법: t분포와 부트스트래핑 본문
이번 글에서는 A/B 테스트를 비롯한 데이터 과학에서 자주 사용되는 신뢰구간이 등장한 이유를 알아봅니다. 또한, 신뢰구간의 t-분포 기반 방법과 부트스트래핑 기법을 비교하여 설명합니다. 부트스트래핑은 컴퓨터 자원을 활용한 현대적 방법으로, 데이터 과학에서 왜 중요한지를 알아봅시다.
1. 글목차
- 점추정의 한계와 구간 추정의 필요성
- 신뢰구간의 등장
- 현재 데이터과학에서 부트스트래핑의 중요성
2. 본문
2.1. 점추정의 한계와 구간 추정의 필요성
통계학의 기본은 모집단을 알아내는 방법론입니다. 하지만 모집단에 대한 전수조사가 불가능에 가깝기 때문에 표본을 가지고 모집단에 대한 특징 평균,표준편차를 구하는 것이 추론통계의 기초라고 하겠습니다 . 표본데이터로 모평균은 쉽게 구할 수 있는 법칙이 있는데 Law of Large Number 라는 대수의 법칙으로 표본 평균은 표본의 크기가 증가할수록 모평균에 수렴하는 경향을 나타낸다는 법칙입니다.
다음은 대수의 법칙을 확인하기 위하여 동전 뒤집기를 예시를 10000번 수행해가면서 평균이 0.5로 수렴하는 그래프입니다.
import random
import matplotlib.pyplot as plt
def law_of_large_numbers(n_trials):
heads_counts = []
proportions = []
for i in range(1, n_trials + 1):
flip_results = [random.randint(0, 1) for _ in range(i)] # 0: tails, 1: heads
heads_count = sum(flip_results)
heads_counts.append(heads_count)
proportions.append(heads_count / i)
plt.figure(figsize=(10, 6))
plt.plot(range(1, n_trials + 1), proportions)
plt.axhline(y=0.5, color='r', linestyle='--', label='Expected Proportion (0.5)')
plt.xlabel('Number of Trials')
plt.ylabel('Proportion of Heads')
plt.title('Law of Large Numbers Demonstration (Coin Flips)')
plt.legend()
plt.grid(True)
plt.show()
law_of_large_numbers(10000)
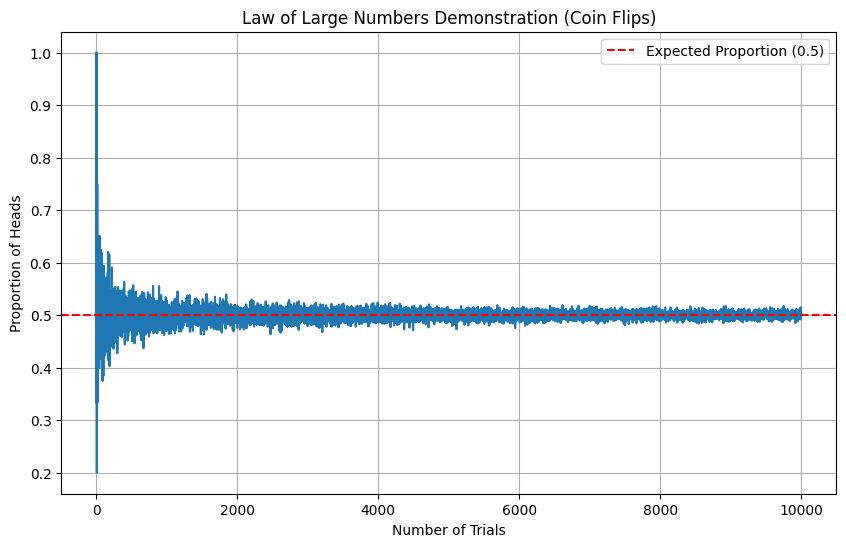
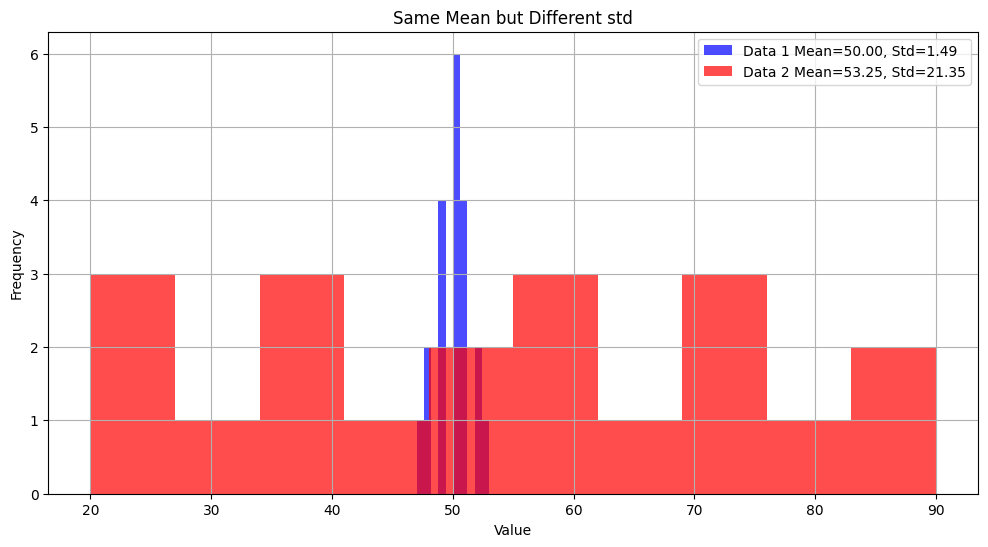
그런데 단순히 표본평균이 같다는 이유로 같은 분포라고 할 수 있을까? 라는게 구간 추정의 등장의 이유입니다. 데이터의 산포도(분산이나 표준편차)가 다르다면, 평균만으로는 데이터를 완전히 설명하기 어렵기 때문입니다. 구간 추정은 이러한 불확실성을 포함하여 데이터를 표현하는 방법론으로 등장하게 되었습니다.
다음은 두 평균이 비슷한 두 데이터가 산포도가 다른 예시입니다.
import numpy as np
import matplotlib.pyplot as plt
data1 = [48, 49, 50, 51, 52, 47, 53, 49, 50, 51, 50, 49, 50, 51, 50, 48, 49, 51, 52, 50] # Low variance
data2 = [30, 40, 50, 60, 70, 20, 80, 45, 55, 65, 35, 75, 25, 85, 50, 60, 40, 70, 20, 90] # High variance
# 평균과 표준편차 계싼
mean1, std1 = np.mean(data1), np.std(data1, ddof = 1)
mean2, std2 = np.mean(data2), np.std(data2, ddof = 1)
# 값 출력
print(f"Data 1 평균 = {mean1:.2f}, 표준편차 = {std1:.2f}")
print(f"Data 2 평균 = {mean2:.2f}, 표준편차 = {std2:.2f}")
# 히스토그램 그리기
plt.figure(figsize=(12, 6))
plt.hist(data1, bins=10, alpha=0.7, label=f"Data 1 Mean={mean1:.2f}, Std={std1:.2f}", color="blue")
plt.hist(data2, bins=10, alpha=0.7, label=f"Data 2 Mean={mean2:.2f}, Std={std2:.2f}", color="red")
plt.title("Same Mean but Different std")
plt.xlabel("Value")
plt.ylabel("Frequency")
plt.legend()
plt.grid(True)
plt.show()
'''
Data 1 평균 = 50.00, 표준편차 = 1.49
Data 2 평균 = 53.25, 표준편차 = 21.35
'''
그렇다면 점추정된 평균을 단순히 제시하는 것보다 구간을 포함하여 표현하는게 더 Data Scientific한 방법론이라고 할 수 있겠습다. 그러면 구간을 잘 표현한다는 것은 무엇일까요?
무작위로 선택된 30명의 남성의 평균 키가 170이라고 해봅시다. 표본평균을 구했으니 구간을 포함하여 설명할 때, 남성은 0 cm ~ 200cm에 반드시 존재합니다. 라고한다면 이는 별로 좋은 표현방법이 아닐 것입니다. 따라서, 좀 더 "합리적인" 표현방법이 필요하게 되었습니다.
2.2. 신뢰구간의 등장
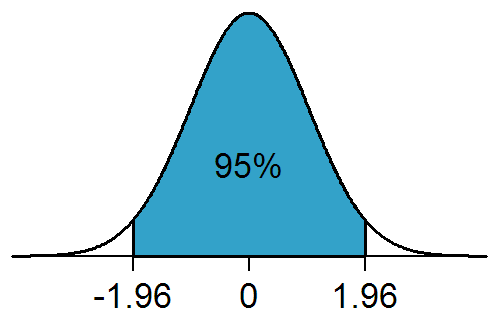
신뢰구간은 정규분포를 기반으로 계산되며, 이를 위해 Z-점수(Z-score)를 사용합니다. 전체 데이터의 95%정도만 설명한다고 하면 표준정규분포 Z score 를 기준으로 +- 1.96의 값에 해당하는 수치를 이용해서 신뢰구간 추정이 가능합니다.
만약 모표준편차를 안다면 다음식으로
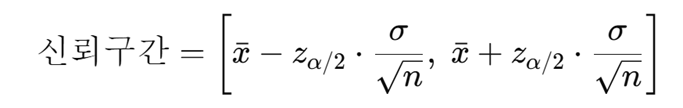
모 표준편차를 모른다면 표본 표준편차를 가지고 대체하여 계산합니다.
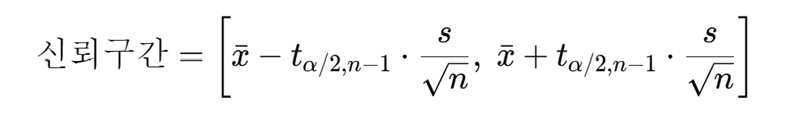
코드로 구현하자면 다음과 같습니다.
import numpy as np
from scipy import stats
korean_men_heights = [
170, 172, 174, 168, 176, 175, 169, 171, 173, 177,
165, 180, 178, 174, 172, 173, 169, 168, 176, 175
]
# 표본 평균구하기
sample_mean = np.mean(korean_men_heights)
sample_std = np.std(korean_men_heights, ddof=1) # ddof=1 for sample std
# 데이터사이즈
n = len(korean_men_heights)
# 표준오차 구하기
standard_error = sample_std / np.sqrt(n)
# 95% 신뢰구간 구하기
confidence_level = 0.95
t_critical = stats.t.ppf((1 + confidence_level) / 2, df=n-1) # t critical value
margin_of_error = t_critical * standard_error
confidence_interval = (sample_mean - margin_of_error, sample_mean + margin_of_error)
# Print results
print("Point and Interval Estimation for Korean Men's Height:")
print(f"Sample Mean: {sample_mean:.2f} cm")
print(f"Sample Standard Deviation: {sample_std:.2f} cm")
print(f"Sample Size: {n}")
print(f"Standard Error: {standard_error:.2f} cm")
print(f"Margin of Error: {margin_of_error:.2f} cm")
print(f"95% Confidence Interval: ({confidence_interval[0]:.2f}, {confidence_interval[1]:.2f})")
'''
Point and Interval Estimation for Korean Men's Height:
Sample Mean: 172.75 cm
Sample Standard Deviation: 3.82 cm
Sample Size: 20
Standard Error: 0.85 cm
Margin of Error: 1.79 cm
95% Confidence Interval: (170.96, 174.54)
'''결과적으로 신뢰구간 95%라는 뜻은 전체 모집단에서 100번 추출을 수행할 때 해당 통계량은 95번 신뢰구간에 들어온다는 뜻이다. 신뢰구간은 편리했지만 가정이 필요했습니다. 바로, 표본 데이터가 정규분포를 따르거나 충분히 큰 표본을 가지고 있어야만 계산이 가능하다는 가정이 필요했습니다.
이는 컴퓨터가 등장하기 이전의 상황이라고 할 수 있습니다. 컴퓨터파워가 높아진 현재는 부트스트래핑방법을 이용하여 신뢰구간을 구하기 시작했습니다.부트스태립(bootstrap)이란 '외부의 도움 없이 스스로'라는 사전적인 정의를 가진 방법론으로 표본 데이터에서 복원추출을 통해서 데이터셋을 생성하여 마치 모집단에 있을법 하지만 새로운 데이터셋을 만드는 방법론입니다. 대표적으로 Random Forest는 이 부트스트랩에 집계를 더한 배깅 방법으로 고안되었습니다.

절차는 다음과 같습니다.
- 데이터에서 복원추출 방식으로 크기 n인 표본을 뽑는다.(재표본추출)
- 재표본 추출한 표본에 대해서 평균을 구한다.
- 1~2번을 10000번 반복한다.
- 95% 신뢰구간을 구하기 위하여 10000개의 표본결과 분포 양쪽 끝 2.5%, 97.5%의 백분율을 구한다.
# 평균과 표준편차
sample_mean = np.mean(korean_men_heights)
sample_std = np.std(korean_men_heights, ddof=1) # ddof=1 for sample std
# 부트스트래핑 파라미터 정하기
n = len(korean_men_heights)
n_bootstraps = 10000
bootstrap_means = []
#부트스트래핑 시행
np.random.seed(42)
for _ in range(n_bootstraps):
bootstrap_sample = np.random.choice(korean_men_heights, size=n, replace=True)
bootstrap_means.append(np.mean(bootstrap_sample))
# 부트스트래핑으로 신뢰구간 구하기
confidence_level = 0.95
lower_bound = np.percentile(bootstrap_means, (1 - confidence_level) / 2 * 100) # 2.5%
upper_bound = np.percentile(bootstrap_means, (1 + confidence_level) / 2 * 100) # 97.5%
bootstrap_confidence_interval = (lower_bound, upper_bound)
# 결과출력
print("Bootstrap Confidence Interval for Korean Men's Height:")
print(f"Sample Mean: {sample_mean:.2f} cm")
print(f"Sample Standard Deviation: {sample_std:.2f} cm")
print(f"95% Confidence Interval (Bootstrap): ({bootstrap_confidence_interval[0]:.2f}, {bootstrap_confidence_interval[1]:.2f})")
'''
Bootstrap Confidence Interval for Korean Men's Height:
Sample Mean: 172.75 cm
Sample Standard Deviation: 3.82 cm
95% Confidence Interval (Bootstrap): (171.15, 174.35)
'''t분포를 이용한 값과 부트스트래핑을 이용한 방법이 유사한 결과를 나타냄을 볼 수 있습니다.
2.3. 현대 데이터과학에서 부트스트래핑의 중요성
Product analyst 의 방법론 중 A/B test는 부트스트래핑의 혜택을 받은 방법 중 하나이다. 일반적으로 A/B test는 두 웹페이지의 방문 비율의 차이 등을 검정하는 경우가 많은데 비율의 차이가 항상 정규분포를 따르는 것은 아니며, 대부분 비대칭이거나 이항분포를 따르는 경우가 많습니다. 이처럼, 부트스트래핑은 데이터의 분포에 관계없이 적용가능하며, 복잡한 통계량에도 유연하게 사용할 수 있다는 점이 장점입니다.
여담으로 Seaborn 의 Error bar 튜토리얼을 보면 신뢰구간(c.i.)를 부트스트래핑으로 계산된다는 걸 확인할 수 있습니다.
3. 출처와 링크
'Data Science' 카테고리의 다른 글
| 글쓰기 커뮤니티 글또, 참가자부터 운영진까지의 3년 간 회고 (1) | 2025.03.30 |
|---|---|
| 왜 프로덕트 팀은 A/B테스트를 사랑할까? (feat 인과추론) (1) | 2025.01.18 |
| ADP 32회 시험 후기와 복기 (0) | 2024.10.13 |
| 글또 10기를 시작하며 다짐 글 (1) | 2024.10.13 |
| 2024년 데이터 직군이 나가야 할 방향 정리하기 ft. AI시대 데이터직군 생존 전략 (0) | 2024.08.20 |



