| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Toastmaster
- 엘뱌키안
- F분포
- 정형데이터
- 데이터
- CC#5
- SQLD
- 2018계획
- 데분
- 취업
- 대중연설
- 인과추론
- 평창
- 풀러스
- 토스트마스터
- 영어연설
- 카이제곱분포
- 데이터분석
- 공유경제
- 연설
- 사이허브
- PGTM
- 제약
- Public Speaking
- 영화
- 임상통계
- 구글#빅쿼리#데이터분석
- 분석
- CC#3
- publicspeaking
- Today
- Total
지지플랏의 DataScience
(1) 선형대수: 선형대수의 활용분야와 벡터 본문
통계에 관련된 책이나 분석방법을 찾다보면 자연스럽게 선형대수학에 대한 개념이 나오게 된다. 이번에는 khan Academy와 개발자를 위한 선형대수학 책을 병행학습하며 기초에 대해서 정리해보고자 한다.
1. 글목차
- 기본개념
- 데이터분석의 활용 분야
- 벡터
2. 본문
2.1. 기본 개념
세상에는 두가지 값이 존재한다. 크기만 존재하는 값을 의미하는 스칼라(Scala), 크기와 방향이 존재하는 벡터(Vector). 이과 전공으로 물리학에서 자주 등장하는 힘에 관련된 표기를 흔히 벡터로 표기하기 때문에 익숙하다.

- 선형대수학(Linear Algebra)는 이처럼 벡터와 행렬, 선형 변환과 같은 수학적인 구조를 다루는 학문이다. 통계학과에서는 2학년의 전공 필수 과목이다.

선형은 직선처럼 행동하는 성질을 뜻하며, 벡터와 행렬 연산에서 입력이 변할 때 비례적으로 변하는 특성을 가짐을 의미한다. 반면 대수는 원소들의 연산 규칙을 이용하여 복잡한 수학구조를 다룰 수 있게한다. 선형대수에서는 벡터 공간안에서 행렬, 선형 변환과 같은 대수적 구조를 연구하는 학문이다.
- 벡터(Vector)는 크기와 방향을 갖는 수학적 개체로 n-차원 공간에 한 점을 나타나는 배열이다.
- 행렬(Matrix)은 숫자들을 직사각형 모양의 배열로 나타낸 수학 구조이며, 벡터의 선형변환이나 여러 방정식을 하나의 시스템으로 묶어 처리하는데 사용된다. 기하학적으로는 벡터의 선형 변환을 적용하는 도구이다.

- 선형 변환(Linear Transformation)은 벡터나 행렬을 변환하는 함수로, 공간에서 점들을 다른 위치로 이동시키는 방법이다.
2.2. 활용 분야
- 데이터는 벡터와 행렬로 표현되므로 데이터분석을 하는 툴의 기본은 이런 선형대수의 이론을 기반으로 한다.
- 선형 회귀 분석은 가장 기본적인 예측 모델 중 하나라 선형 방정식을 기반으로 한다.
$\hat{y} = X \beta $
- 차원축소 방법 중 하나인 주성분 분석(PCA)은 행렬의 고유값과 고유벡터의 계산을 통해 데이터의 주된 변동을 설명하는 축을 찾아내어 데이터의 차원을 줄인다. 해당 내용은 데이터과학을 위한 통계 스터디에 정리한 바 있다.
https://snowgot.tistory.com/134
(9) DSforS : Chap5. 분류 5.1 ~ 5.3 나이브베이즈(NB), 선형판별분석(LDA)
1. 목차5.1. 나이브베이즈(NB)5.2. 선형판별분석(LDA) 2. 본문 들어가기에 앞서 이책이 이론적으로는 확실히 친절한 책은 아님을 다시 확인시켜주는 단원이라 생각된다. 특히 나이브 베이즈와 판별
snowgot.tistory.com
- 추천시스템(Recommendation System)은 행렬 분해(Matrix Factorization) 방법을 사용하여 사용자와 아이템 간이 상호작용 행렬을 분해아여 숨겨진 패턴을 발견한다. 예를들어 특이값 분해(Sigular Value Decomposition)은 추천 시스템에서 자주 사용 되는 기법이다.
- 클러스터링 및 분류: K-means 클러스터링과 같은 군집화는 벡터 간의 유사도를 계산하기 위하여 유클리드 거리 혹은 코사인 거리가 사용된다. 이때 연산이 선형대수 기반이다.
2.3. 벡터(vector)
- 표기법: 일반적으로 진한 로마자 $v$ 혹은 이탤릭체 $v$, 위쪽에 화살표 $\overrightarrow{v}$를 붙여 표기한다.
- 차원(dimensionality): 벡터가 가진 원소의 수. 차원은 일반적으로 $\mathbb{R}$ 으로 나타내는데 $\mathbb{R}^2$ 와 같이 표현하면 실수(Real Number) 2차원 평면(흔히 말하는 x,y축)에 존재한다는 것이다.
- 방향(orientation) : 열방향 혹은 행방향으로 나타낸다.
- 벡터는 시작점이 일반적으로 원점을 기준으로 표기하며, 방향과 크기만 같다면 모두 같은 벡터이다.

- 방향이 존재하기 때문에 벡터는 기하학적 공간에 표기하여 설명을 할 수 있는 장점이 있다. 대표적으로 벡터의 덧셈과 뺄쌤은 다음과 같이 표기한다.
- 벡터는 시작점이 일반적으로 원점을 기준으로 표기하며, 방향과 크기만 같다면 모두 같은 벡터이다.


- 크기(norm): 는 벡터의 꼬리부터 머리까지의 거리이며 일반적으로 유클리드 공식에 따라 구한다. 크기는 양쪽에 | 2개로 표기한다.
$ \left\|v \right\| = \sqrt{\sum_{i=1}^{n}{v_{i}^2}} $
- 단위 벡터: 길이가 1인 벡터로 어떤 벡터든 크기기로 나누면 길이를 1로 제한하여 만들 수 있다.
$ \left\|v \right\| =1 $
- 벡터의 내적(dot product)
- 벡터의 내적은 점곰(dot product) 혹은 스칼라 곱이라고도 표현하며, 동일한 차원의 두 벡터사이에서 수행할 수 있다. 예를 들면 [1 2] $\cdot $ [1, 3 ] = 1*1 + 2*3 = 7 이 된다. 내적한 값은 방향이 존재하지 않은 스칼라 값이 된다. 시그마 표기법을 이용한 공식은 다음과 같다.
$ \vec{v} \cdot \vec{w} = \sum^n_{i = 1}{a_i b_i}$
Python에서는 numpy의 np.dot 함수로 구할 수 있다.
import numpy as np
v = np.array([1,2])
w = np.array([1,3])
np.dot(v,w)
# 7벡터의 내적은 두 벡터의 유사성과 매핑의 척도이다. 몸무게와 키의 데이터를 수집했다고 했을때 각 벡터의 내적은 클 것이다. 하지만 단위가 크면 해당 값도 클 것이기 때문에 각 벡터의 크기로 정규화로 제거할 수 있다. 이런 정규화된 내적을 피어슨 상관계수 라고 한다.
- 내적의 기하학적 해석
- 내적을 벡터 기호를 이용하여 표기하면 다음과 같다.
$ \overrightarrow{v} \cdot \overrightarrow{w} = \left\| v \right\| \left\|w \right\| cos(\theta) $
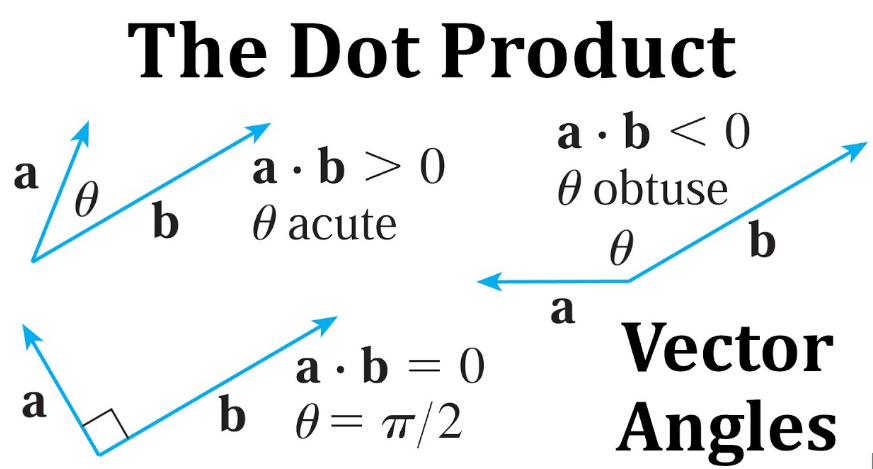
여기서 $ \overrightarrow{a}*cos(\theta)$ 는 $ \overrightarrow{v}$의 $ \overrightarrow{b}$의 정사영(projection)임을 확인할 수 있다. (삼각함수의 성질)
- 백터의 외적(Corss product)
- 벡터의 외적 크로스 곱이라고 말하며, $vw^{T}$로 나타낸다. 기본적으로 벡터는 열방향으로 표기하므로 전치(Transporse)를 통해 행방향으로 바꿔주기 위함이다. 또한, 외적은 내적과 달리 3차원 공간에서만 정의된다.
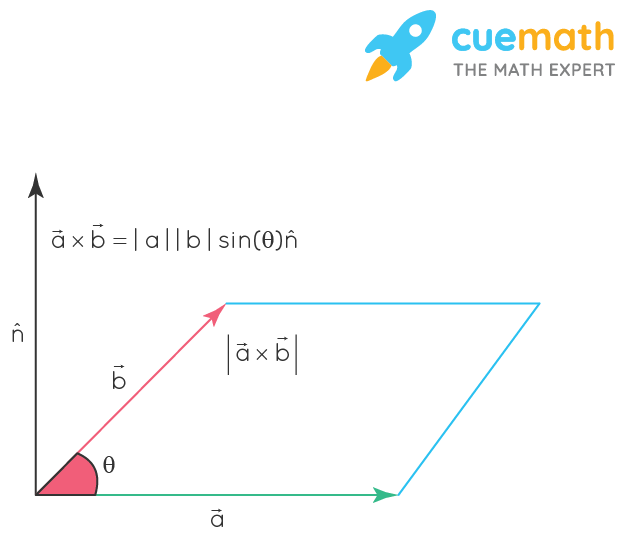
$ \|\vec{v} \times \vec{w}\| = \|\vec{v}\| \cdot \|\vec{w}\| \cdot \sin \theta $
import numpy as np
v = np.array([1,2,3])
w = np.array([1,4,5])
np.cross(v, w.T)
# array([-2, -2, 2])- 외적의 기하학적 해석
- 외적은 3차원 공간에서 두 벡터가 만들어 내는 평면의 법선 벡터이다
- 직교 벡터 분해
- 행렬의 특징 중 하나는 분해를 통해 행렬에 숨겨진 정보를 찾을 수 있다는 점이다. 마치 실수는 정수와 소수점 부분으로 나눌 수 있고, 수는 소인수 분해를 통해서 소수로 나눌 수 있는 것 처럼
- ex) 4.27 -> 4 + 0.27
- ex2) 16 -> $ 2^4$
- 원리: 두 벡터가 있을 때, 한 벡터를 다른 벡터에 직교하는 벡터를 만들려면 어떻게 해야할까? 아래 $ \overrightarrow{b}$ 의 벡터를 $ \overrightarrow{a} $ 에 직교하도록 하려면, 상수배 ($\beta$)를 한 $ \overrightarrow{a}$를 만들고 두 벡터의 차이를 구하면 된다. 두 벡터의 차이가 직교하면 내적이 0 이되므로 다음 식이 성립한다.
- 행렬의 특징 중 하나는 분해를 통해 행렬에 숨겨진 정보를 찾을 수 있다는 점이다. 마치 실수는 정수와 소수점 부분으로 나눌 수 있고, 수는 소인수 분해를 통해서 소수로 나눌 수 있는 것 처럼
$ a^{T}(b-\beta{a}) = 0 $
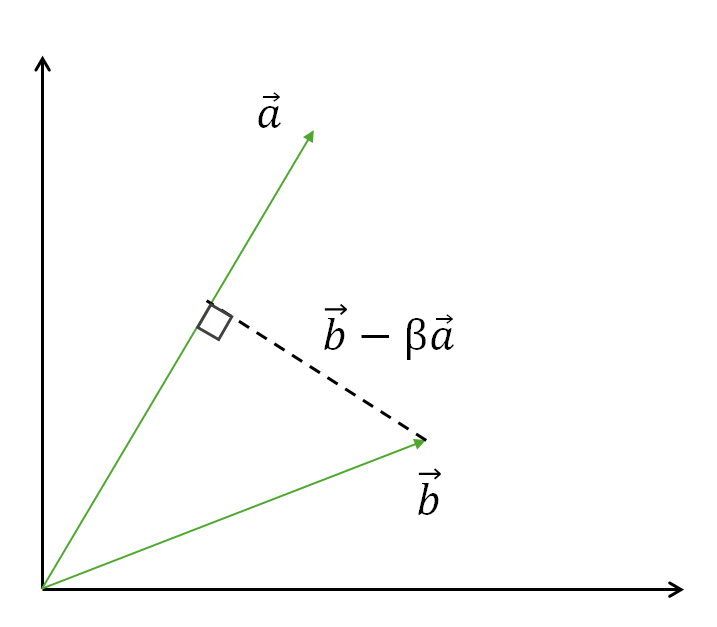
$\beta$를 구하기 위하여 내적이 분배 법칙이 가능하다는 점을 응용한다면 다음 식에 도달하게 된다.
$ a^{T}b - \beta a^{T}a = 0 $
$ \beta a^{T}a = a^{T}b $
$ \therefore \beta = \frac{a^{T}b}{a^{T}a} $
위식 $\beta$는 선형회귀의 $\beta$와 같은 기호이다. 위 식은 벡터 b를 a에 투영하여 그 투영 성분을 제거해 a와 직교하는 방법만 남기는 방법이다. 직교한다는 것은 기존 데이터(a벡터)를 설명하지 못하는 오차(잔차)를 말하며 바로 $ a^{T}b - \beta a^{T}a$ 벡터가 잔차 성분이다. 이처럼 행렬분해와 직교화는 최소제곱법, 통계학, 머신러닝에 걸쳐 이루는 많은 응용의 기반이 된다.
'Data Science > Khan Academy' 카테고리의 다른 글
| (9) Khan Academy 카이제곱분포와 검정과 F분포와 분산분석 (0) | 2024.08.19 |
|---|---|
| (8) Khan Academy: 유의성 검정과 절차, 통계방법론 정리 (0) | 2024.08.12 |
| (7) Khan Academy: 11단원 모평균과 모비율 추론, 신뢰구간 (0) | 2024.08.04 |
| (5) Khan Academy: 9단원 확률변수 (0) | 2024.07.31 |
| (4) Khan Acadmey: 단원7,8: 조합,순열 그리고 확률에 관련된 기호들 (1) | 2024.07.22 |




