| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 공유경제
- 연설
- 제약
- 인과추론
- 엘뱌키안
- 취업
- 영어연설
- 분석
- CC#5
- 구글#빅쿼리#데이터분석
- 평창
- 2018계획
- 데이터분석
- 대중연설
- 데분
- Public Speaking
- PGTM
- F분포
- 데이터
- 토스트마스터
- 정형데이터
- 카이제곱분포
- 사이허브
- publicspeaking
- 영화
- CC#3
- SQLD
- Toastmaster
- 풀러스
- 임상통계
- Today
- Total
지지플랏의 DataScience
(6) Chapter 5: 매칭 Part1: 성향 점수(PS), 역확률 가중치(IPW) 본문
(6) Chapter 5: 매칭 Part1: 성향 점수(PS), 역확률 가중치(IPW)
지지플랏 2024. 10. 7. 18:12지난 글에서는 선형회귀분석을 사용하여 교란요인을 보정하는 방법과 온라인 실험상에서의 활용 방법을 알아보았습니다. 이번에는 또 다른 편향 방법 중 하나인 성향 점수 가중치(propensity weighting)에 대해서 알아보고 실제 예시로 구현해보겠습니다.
1. 글목차
- 매칭의 필요성
- 매칭의 정의
- 방법1: 성향점수(PS)
- 방법2: 역확률 가중치(IPW)
2. 본문
2.1. 매칭(Matching)의 필요성
교육프로그램의 효과를 측정하기 위해서 교육과정에서 얻은 데이터가 있습니다. 우리의 목적은 교육을 받은 사실(처치변수)과 직원 참여도(결과변수) 간의 인과관계를 추정하여 실제적으로 교육 프로그램이 효과가 있는지 확인할 예정입니다.
navie하게 단순성형회귀로 표준화된 참여점수(종속변수) ~ 처치변수(독립변수)에 관한 회귀분석을 진행하면 다음과 같습니다.
import pandas as pd
import numpy as np
df = pd.read_csv('./data/management_training.csv')
df.head(3)
$ engagement_{i} = \tau T_{i} + e_{i} $
import statsmodels.formula.api as smf
smf.ols('engagement_score ~ intervention', data = df).fit().summary().tables[1]
하지만 위의 식에서는 교란변수를 보정하지 않았으므로 실제로 직원교육이 직원 참여도에 0.43만큼 영향이 있다고 단언하기 어렵습니다. 4장에서 배웠던 것처럼 교란변수를 보정하여 결과를 내보겠습니다.
위의 교육프로그램에 대한 영향의 식에 교란변수까지 포함하여 식을 세우면 다음과 같습니다.
$engagement_{i} = \tau T_{i} + \theta X_{i} + e_{i} $
model = smf.ols("""engagement_score ~ intervention
+ tenure + last_engagement_score + department_score
+ n_of_reports + C(gender) + C(role)""", data=df).fit()
print("ATE:", model.params["intervention"].round(3))
print(f"95% CI:", model.conf_int().loc["intervention", :].values.T.round(3))
"""
ATE: 0.268
95% CI: [0.234 0.302]
"""이전의 ATE효과 보다 훨씬 작아진 것을 볼 수 가 있습니다. 따라서, 단순히 참여 여부에 대해서만 추정하게 되면 직원참여도가 높은 관리자가 교육 프로그램에 더 많이 참여 했을 가능성이 있다는 해석을 할 수 있습니다.
하지만 이러한 교란변수 보정이 모든 변수의 상호작용 관계를 설명할 수 있는 것은 아닙니다. 예컨데 선형회귀모델은 처리변수(T)와 결과변수(Y)의 관계가 선형적이라고 가정합니다(① 선형성 가정). 다시 말해 두 변수가 비선형적이라면 인과효과를 정확하게 추정하지 못합니다. 또한, 교란 변수들 간의 비선형성 혹은 상호작용(interaction)을 담지 못합니다.(② 교란변수 모형화의 한계)
이러한 선형회귀 모델의 가정에 대한 의존성을 줄이는 방법으로, 처리군과 대조군을 유사하게 만드는 PS matching 혹은 데이터를 활용하면서 처리 여부에 따른 공변량 차이를 균형있게 조절하는 IPW 방법을 통해서 더 나은 인과 추정을 노려볼 수 있겠습니다.
2.2. 매칭의 정의
매칭이란?
- 관찰 데이터에서 처리군과 대조군의 특성 차이를 줄여주어 인과 효과를 추정하는데 사용되는 기법
매칭을 사용하는 이유는 관찰연구이거나 혹은 A/Btest에 준하게 실험상황을 가정했는데도 불구하고 불응(non-compliance)등으로 관찰연구와 비슷하게 되었을 때 활용할 수 있기 때문입니다. 매칭은 선택 편향(Selection Bias)을 최소화하는 하나의 방법입니다.
예컨데, 교육 프로그램의 효과를 평가할 때 프로그램에 자발적으로 참여한 사람들은 참여하지 않은 사람들보다 더 높은 동기나나 학업 성취에 대한 관심이 있을 수 있습니다. 이런 상태에서 단순히 두 그룹의 평균을 비교하는 것은 교육 프로그램의 효과가 아니라 참여 동기로 인한 결과 차이를 반영하게 되어 인과적 결론을 잘못 내릴 수 있습니다.
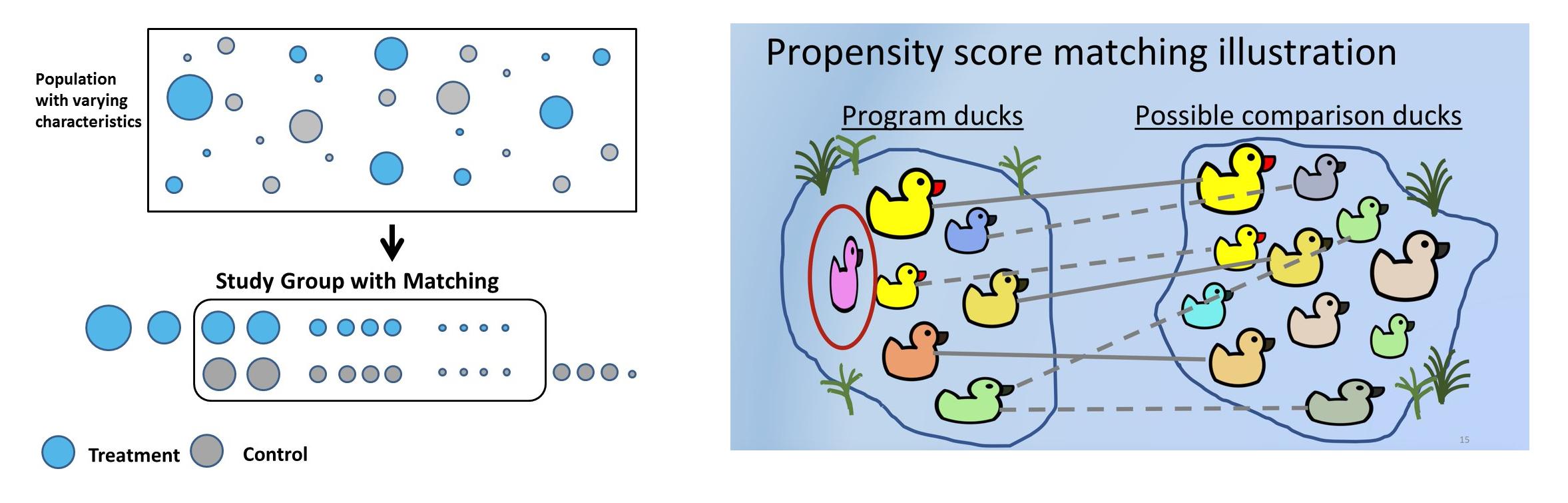
2.2. 방법1: 성향 점수(Propensity Score)
기존에는 교란변수($X$)를 식별하여 조건부로 두어 뒷문 경로를 차단했다면, 이번에는 성향 점수($e(x)$)를 조건부로 두어 다음 식을 성립하게 하는 목적이 있습니다.
$ (Y_{1}, Y_{0}) \perp P(x)$

- 정의: 개체가 처리를 받을 확률을 나타내는 값. 로지스틱 회귀와 같은 모델을 사용해 추정할 수 있음
- 아이디어: 공변량 들의 고차원 정보를 하나의 요약된 값으로 표현하여 마치 차원 축소를 진행하여 차원의 저주의 문제를 줄여주게 함
- ps score : $ \hat{e}(X) = P(T=1 | X = x) $
- $\hat{e}(X)$: 성향점수 추정치, 이상적인 값
ps_model = smf.logit("""intervention ~
tenure + last_engagement_score + department_score
+ C(n_of_reports) + C(gender) + C(role)""", data=df).fit(disp=0)
data_ps = df.assign(
propensity_score = ps_model.predict(df),
)
data_ps[["intervention", "engagement_score", "propensity_score"]].head()
model = smf.ols("engagement_score ~ intervention + propensity_score",
data=data_ps).fit()
model.params["intervention"].round(3)
"""
0.263
"""결과적으로 교란변수를 보정한 선형회귀의 식과 유사한 ATE를 추정할 수 있음을 알 수 있습니다.
2.3. 역확률 가중치(IPW)
- 정의: 개체가 처리를 받았을 확률(성향 점수)의 역수를 사용하여 계산. 예를들어 어떤 개체가 처리 받을 확률이 낮다면 그 개체의 가중치는 높아지는 식
- 아이디어: 처치의 역확률에 따라 데이터의 가중치를 보정하여, 처치가 무작위 배정된 것처럼 보이게 함
$w_{i} $ = \begin{cases} \frac{1}{e(X_i)}, & \text{if } T_i = 1 \ (\text{처리군}) \\ \frac{1}{1 - e(X_i)}, & \text{if } T_i = 0 \ (\text{대조군}) \end{cases}
weight_t = 1/data_ps.query("intervention==1")["propensity_score"]
weight_nt = 1/(1-data_ps.query("intervention==0")["propensity_score"])
t1 = data_ps.query("intervention==1")["engagement_score"]
t0 = data_ps.query("intervention==0")["engagement_score"]
y1 = sum(t1*weight_t)/len(data_ps)
y0 = sum(t0*weight_nt)/len(data_ps)
ATE = y1 - y0
print(f"E[Y1]:{y1:.3f}")
print(f"E[Y0]:{y0:.3f}")
print(f"ATE, {ATE:.3f}")
"""
E[Y1]:0.117
E[Y0]:-0.149
ATE, 0.266
"""얼핏 보면 성향점수(PS) 방법과 역확률 가중치(IPW) 방법이 같은 아이디어에서 나와서 차이가 없는 것 처럼보인다. 다음과 같이 정리해본다.
| 성향 점수(PS) | 역확률 가중치(IPW) | |
| 정의 | 공변량을 사용해 각 개체가 처리받을 확률을 추정, 확률 값 | 성향 점수를 이용하여 개체별로 가중치를 부여하는 방법 |
| 방법 | 처리군과 대조군의 특성이 최대한 비슷하도록 만들어 비교, 데이터 탈락 가능성 有 | 모든 개체에 대해서 계산된 가중치를 부여 |
3. 출처와 링크
- 교보문고 실무로 통하는 인과추론 with python
- Jupyter book 인과추론
- github 가짜연구소 Casual Inference Team
- Youtube 인과추론의 데이터과학
'Data Science > 실무로 통하는 인과추론 with 파이썬' 카테고리의 다른 글
| 인과추론 스터디 KPT 후기 (2) | 2024.10.14 |
|---|---|
| (5) Chapter 4: 유용한 선형회귀 Part2: FWL 방법론 (4) | 2024.09.30 |
| (4) Chapter 4: 유용한 선형회귀 Part 1 - 온라인 마케팅 (3) | 2024.09.23 |
| (3) Chapter 3 그래프 인과모델 (2) | 2024.09.19 |
| (2) Chapter 2 인과추론을 위한 무작위 실험과 기초 통계 (1) | 2024.09.09 |



