| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- F분포
- 데이터
- 사이허브
- 인과추론
- 연설
- 정형데이터
- Toastmaster
- 토스트마스터
- 풀러스
- 제약
- 분석
- Public Speaking
- 데이터분석
- 공유경제
- 영화
- 2018계획
- 취업
- 카이제곱분포
- 엘뱌키안
- 구글#빅쿼리#데이터분석
- 대중연설
- 평창
- CC#5
- publicspeaking
- 데분
- PGTM
- 영어연설
- SQLD
- CC#3
- 임상통계
- Today
- Total
지지플랏의 DataScience
(4) Chapter 4: 유용한 선형회귀 Part 1 - 온라인 마케팅 본문
1장에서는 인과추론의 소개, 2장에서는 RCT의 중요성과 기초 통계개념 그리고 3장에서는 인과관계를 표현하는 그래프 인과모델에 대해서 알아보았다. 이번 장에서는 인과관계를 추론하는데 아주 중요한 회귀분석을 알아본다. 회귀분석은 데이터 분석에서 접할 수 있는 가장 간단하지만 파워풀한 통계방법론으로 편향을 줄이는 방법에서도 유용하다. 또한, 온라인 마케팅 모델에서의 실용적인 사례도 알아본다.
1. 글목차
- A/B test 결과 회귀분석 적용
- 온라인 마케팅에서의 회귀분석
2. 본문
2.1. A/B test 결과 회귀분석 적용
온라인 스트리밍 서비스를 하는 회사에서 새로운 추천시스템을 개발했고 이를 측정하기 위해서 A/Btest를 수행했다. 이를 단순집계와 선형회귀의 결과로 표현해보자.
import pandas as pd
data = pd.read_csv('./rec_ab_test.csv')
data.head()
다음은 단순 선형회귀의 식과 구현 결과이다.
$ WatchTime_{i} = \beta_{0} + \beta_{1}challenger_{i} + e_{i} $
import statsmodels.formula.api as smf
#C()카테고리 변수 처리
#상수항을 따로 넣지 않아 watch_time은 recommender 변수에만 의존 한다고 가정함.
result = smf.ols('watch_time ~ C(recommender)', data = data).fit()
result.summary().tables[1]
다음은 추천시스템 유무에 따른 평균시청시간 결과이다.
data.groupby('recommender')[['watch_time']].mean()
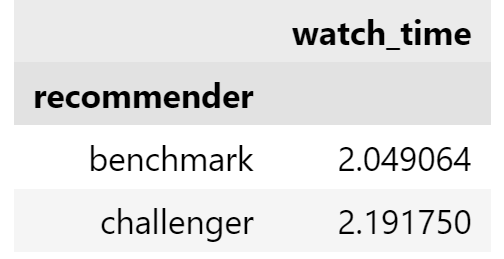
추천시스템을 적용한 그룹은 평균 시청시간이 2.19시간이었고 대조군은 2.05시간이였다. 이는 선형회귀의 결과에서 기본 $\hat{\beta_{0}}$이 2.05 이고 $\hat{\beta_{1}}$(= 추천시스템을 적용했을 때 시청시간의 증가분)가 0.14 라는 값과 일치한다. 이미 a/b test 를 적용한 결과이니 교란변수가 잘 제어되었다는 반증이기도 하다.
2.2. 온라인 마케팅에서의 회귀분석
2.2.1. 온라인 마케팅의 관심사
책에서느 채무 불이행이라는 데이터를 가지고 회귀분석의 이론과 유용성을 설명한다. 필자는 인과추론의 데이터과학이라는 Youtube와 같이 책을 보고 있는데 다음 영상이 매우 실증적인 설명을 잘해주셔서 풀어서 써보려고한다. 링크는 다음과 같다 .
https://www.youtube.com/watch?v=07SWlTOqxpY&t=1s
온라인 마케팅이란 마케팅 목표(신규 고객 유치, 이탈방지)를 수립하고 이 목표를 달성하기 위한 마케팅을 진행하는 과정이며, 가장 중요한 것은 마케팅 예산 투입 대비 얼만큼의 효과가 발생했는지 효율을 측정하는 것이다. 이를 대표한 지표로서 ROAS(Return on Advertisement Spend)이다.
2.2.2. 기존 측정 지표: LTA
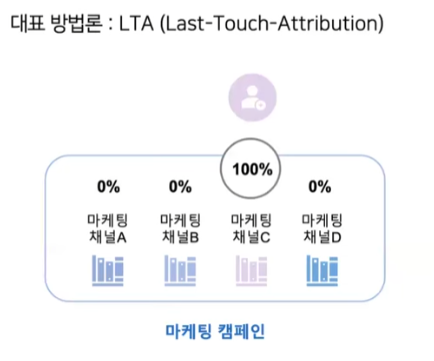
LTA(Last Touch Attribution)은 가장 기본적인 측정 방법으로 마케팅 여러가지 매체(Meta, google, naver)쓰고 노출이 되더라도 마지막에 인입된 경로를 기준으로 측정하는 방법이다. 딱 들어도 naive한 방법이라고 여겨지기 때문에 다음과 같은 한계를 가진다.
- 한계
1. 유저가 거쳐온 여러 종류의 매체 효과를 측정하기 어려움.
2. Touch 이후 전환을 측정할 수 없으면 LTA 측정 불가
ex) 광고를 보고 잠시 있다가 기억이나서 검색해서 들어오는 경우, 광고에 대한 측정 데이터가 남지 않음
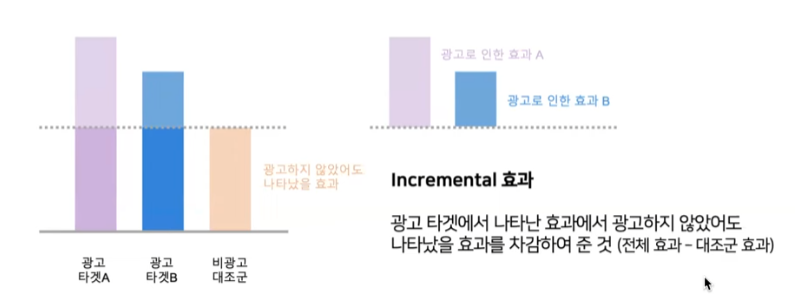
3. 광고의 Incremental(증가분) 측정 불가
ex) 원래 들어오려고 했던 organic유저인가 아니면 마케팅 효과로 들어온 유저인가?-
- 이를 위해서는 비광고 대조군의 영향을 제거해야함. a/btest 를 이용하여 광고 타켓군과 대조군을 분할하여 광고를 집행 해볼 수 있다.
-
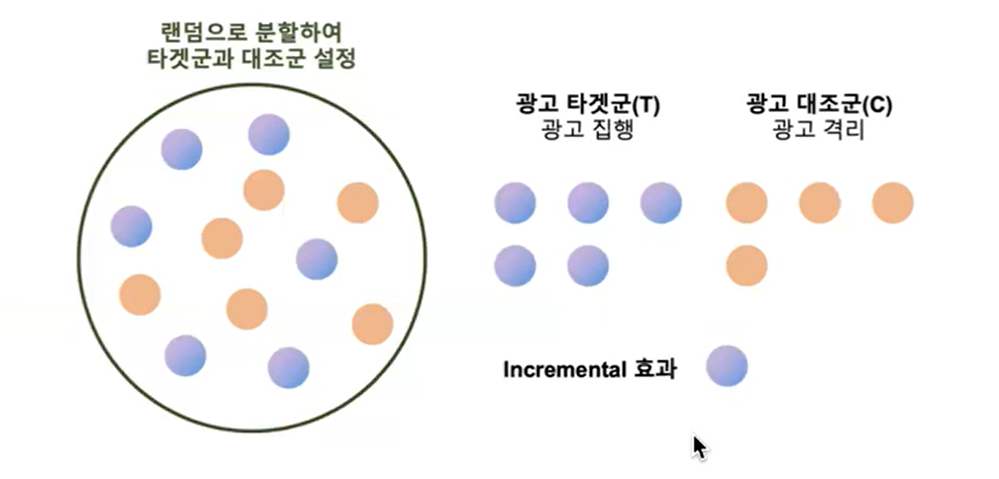
하지만 위 상황에서 우리가 알아야하는 점은 신규유저의 경우 대조군 설정이 불가능하다. 이유는 애초에 데이터가 존재하지 않기 때문이다. 온라인 마케팅은 2가지 UA 마케팅과 리타겟팅 마케팅이 존재하는데 abtest를 적용할 수 있는 마케팅은 리타게팅 마케팅으로 이미 접속한 유저를 재모객하는 온라인 마케팅일 때 유효하다고 할 수 있겠다.

2.2.3. 마케팅 믹스 모델링(MMM)
하지만 abtest는 개별 매체의 성과를 비교하는데 유용하지만, 다채널 환경에서의 복잡성에서는 적용하기 어려운 점이 있다. 또한 abtest가 적용하기 어려운 장기적인 광고효과를 측정하는데도 어려움이 있다. 따라서, 광고의 Incremnental 효과를 측정하면서도 각 매체의 기여도를 파악할 순 없을까? 라는 의문에서 MMM이 시작되었다.
고객 1명을 데리고 오는데 각 마케팅 매체가 어느정도 기여를 했는지 파악
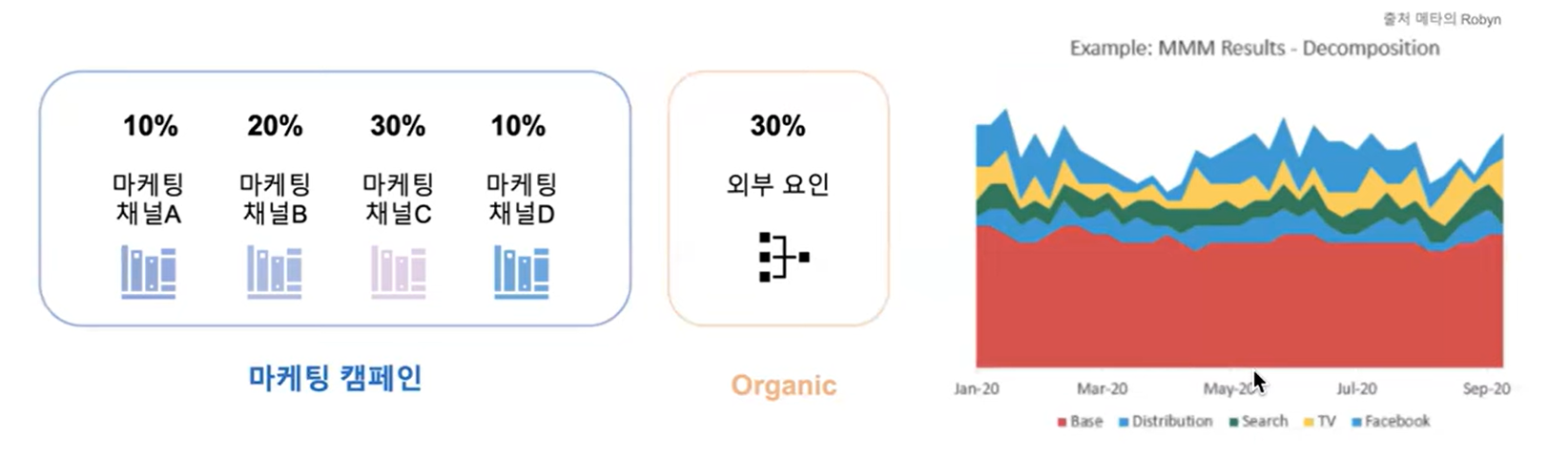
이때 다중선형회귀를 이용해서 모델링한다.
$y_{i} = \beta_{0} + \beta_{1}x_{1} + \beta_{2}x_{2} + ... \beta_{n}x_{n} + \epsilon$
- $x$: 원인변수 외부 매체, 환경 요인)
- $\beta$: 원인 변수의 기여도(마케팅 매체 별 효율)
예를 들어 판매량에 대한 회귀분석을 수립하면 다음과 같다.
$y = \beta_{Never}X_{Never} + \beta_{mechat}X_{mechat} + \beta_{stargram}X_{stargram} + \beta_{makao}X_{makao} + \sum_{i=1}^{12}\beta_{month}I(X_{month} = i) + \epsilon$
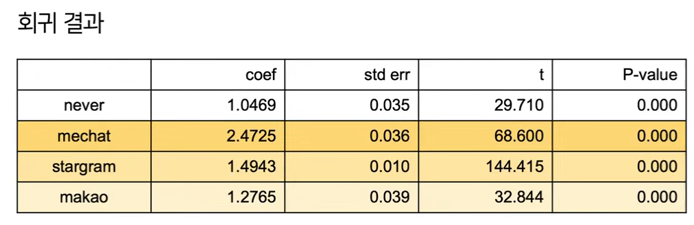
위 결과의 해석은 coef = 1이면 투입 대비 성과가 1:1이라는 것이며, mechat의 효율이 제일 좋고 never의 효율이 제일 좋지 않다고 판단단 내릴 수 있다. 따라서, 마케팅 예산을 mechat에 집중하고 never에 집행 예산을 축소하거나 중단하는 등의 의사결정을 지원할 수 있다.
3. 출처와 링크
- 교보문고 실무로 통하는 인과추론 with python
- Jupyter book 인과추론
- github 가짜연구소 Casual Inference Team
- Youtube 인과추론의 데이터과학
- Github causal-inference-in-python-code
'Data Science > 실무로 통하는 인과추론 with 파이썬' 카테고리의 다른 글
| (6) Chapter 5: 매칭 Part1: 성향 점수(PS), 역확률 가중치(IPW) (3) | 2024.10.07 |
|---|---|
| (5) Chapter 4: 유용한 선형회귀 Part2: FWL 방법론 (4) | 2024.09.30 |
| (3) Chapter 3 그래프 인과모델 (2) | 2024.09.19 |
| (2) Chapter 2 인과추론을 위한 무작위 실험과 기초 통계 (1) | 2024.09.09 |
| (1) Chapter: 인과추론 소개 (5) | 2024.09.02 |




