| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 연설
- CC#5
- 풀러스
- 사이허브
- CC#3
- 구글#빅쿼리#데이터분석
- 영어연설
- 분석
- 데이터
- 엘뱌키안
- 제약
- publicspeaking
- 취업
- Public Speaking
- F분포
- 평창
- 2018계획
- 카이제곱분포
- 데이터분석
- 토스트마스터
- 영화
- PGTM
- SQLD
- Toastmaster
- 인과추론
- 임상통계
- 정형데이터
- 데분
- 대중연설
- 공유경제
Archives
- Today
- Total
지지플랏의 DataScience
생존분석과 lifeline 패키지 활용 - LogRank, 카플란-마이어, 콕스비례위험모형 본문
반응형
1. 생존분석이란
- 시간-이벤트 데이터(예: 생존 시간, 고장 시간 등)를 분석하는 데 사용됨
- 주요 목표는 생존 시간 분포를 추정하고, 생존 시간에 영향을 미치는 요인을 식별하며, 여러 그룹 간의 생존 시간을 비교하는것. 대표적인 방법으로 LogRank, 카플란-마이어 추정법, 콕스 비례위험 모형이 있다.
2.1. 카플란-마이어 추정법 (Kaplan-Meier Estimator)
- 특정 시간까지 이벤트가 발생하지 않을 확률(생존 함수)을 비모수적으로 추정하는 방법
- 각 시간 점에서 생존 확률을 계산하고, 이를 통해 전체 생존 곡선을 작성.
- 사건이 독립적이라는 가정이 있지만, 실제로는 이 가정이 항상 만족되지 않을 수 있음(실제로 병은 누적되는 대미지가 있으므로)
ˆS(t)=∏ti≤t(1−dini)

import pandas as pd
import matplotlib.pyplot as plt
from lifelines import KaplanMeierFitter
# 예시 데이터 생성
data = {
'duration': [5, 6, 6, 7, 8, 8, 10, 12, 14, 15, 18, 20, 25],
'event': [1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1]
}
df = pd.DataFrame(data)
# Kaplan-Meier Fitter 생성
kmf = KaplanMeierFitter()
# 생존 함수 적합
kmf.fit(durations=df['duration'], event_observed=df['event'])
# 생존 곡선 시각화
plt.figure(figsize=(10, 6))
kmf.plot_survival_function()
plt.title('Kaplan-Meier Survival Curve')
plt.xlabel('Time')
plt.ylabel('Survival Probability')
plt.grid(True)
plt.show()
- 결과해석
- 시간에 따른 생존율을 알 수 있음(25 시간 단위에 최저)
- 중위 생존시간은 13 시간단위로 추정됨
3.1. Log-Rank test
- 카플란 마이어 기법의 응용
- 두 그룹 간의 시간에 따른 생존율 차이를 검정하는 방법
- 각 시간 점에서 관찰된 사건 수와 기대 사건 수를 비교하여(카이제곱검정), 두 그룹의 생존 곡선이 통계적으로 유의미하게 다른지를 평가
χ2=(O1−E1)2V1+(O2−E2)2V2

3.2. 실습
- 예시 데이터
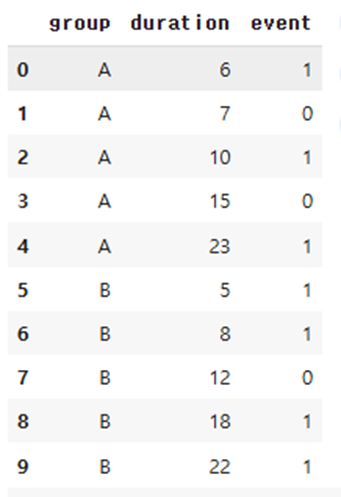
import pandas as pd
from lifelines import KaplanMeierFitter
from lifelines.statistics import logrank_test
# 데이터 생성
data = {
'group': ['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B'],
'duration': [6, 7, 10, 15, 23, 5, 8, 12, 18, 22],
'event': [1, 0, 1, 0, 1, 1, 1, 0, 1, 1]
}
df = pd.DataFrame(data)
# 두 그룹 나누기
groupA = df[df['group'] == 'A']
groupB = df[df['group'] == 'B']
# Kaplan-Meier Fitter 생성
kmf_A = KaplanMeierFitter()
kmf_B = KaplanMeierFitter()
# 생존 함수 적합
kmf_A.fit(durations=groupA['duration'], event_observed=groupA['event'], label='Group A')
kmf_B.fit(durations=groupB['duration'], event_observed=groupB['event'], label='Group B')
# Log-Rank 테스트 수행
results = logrank_test(groupA['duration'], groupB['duration'], event_observed_A=groupA['event'], event_observed_B=groupB['event'])
results.print_summary()
- 시각화 코드
import pandas as pd
import matplotlib.pyplot as plt
from lifelines import KaplanMeierFitter
# 데이터 생성
data = {
'group': ['A', 'A', 'A', 'A', 'A', 'B', 'B', 'B', 'B', 'B'],
'duration': [6, 7, 10, 15, 23, 5, 8, 12, 18, 22],
'event': [1, 0, 1, 0, 1, 1, 1, 0, 1, 1]
}
df = pd.DataFrame(data)
# 두 그룹 나누기
groupA = df[df['group'] == 'A']
groupB = df[df['group'] == 'B']
# Kaplan-Meier Fitter 생성
kmf_A = KaplanMeierFitter()
kmf_B = KaplanMeierFitter()
# 생존 함수 적합
kmf_A.fit(durations=groupA['duration'], event_observed=groupA['event'], label='Group A')
kmf_B.fit(durations=groupB['duration'], event_observed=groupB['event'], label='Group B')
# 생존 곡선 시각화
plt.figure(figsize=(10, 6))
kmf_A.plot_survival_function()
kmf_B.plot_survival_function()
plt.title('Kaplan-Meier Survival Curves')
plt.xlabel('Time (months)')
plt.ylabel('Survival Probability')
plt.legend()
plt.grid(True)
plt.show()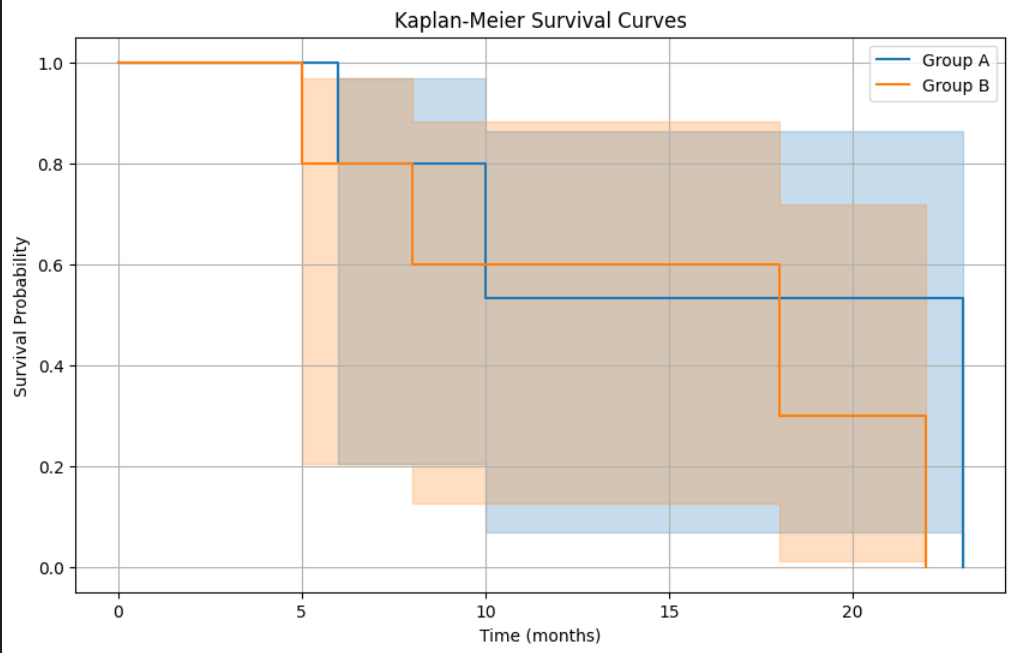
- 결과해석
- 테스트 통계량은 0.46 p-value는 0.50로 귀무가설(두 그룹 간의 생존 곡선에 유의미한 차이가 없다)를 기각하지 못함
- 따라서 그룹 A와 그룹 B의 생존 시간이 통계적으로 유의미하게 다르지 않음을 결론 지을 수 있음
4.1. 콕스 비례 위험 모형 (Cox Proportional Hazards Model)
- 카플란마이어 추정법은 사건이 독립적이라는 가정의 한계 따라서 시간에 따른 사건 발생 위험률(위험 함수)을 모델링
- 공변량(독립변수)이 시간에 따라 비례적으로 위험률에 영향을 미친다는 가정
- 기준 위험률와 공변량의 선형 결합을 지수 함수 형태로 결합하여 위험률을 표현
- 기준위험률(λ0(t)): 시간 t 기준 위험률로 공변량의 영향을 제거한 상태의 기본적인 위험률
- 공변량(Covariates, X): 사건 발생에 영향을 미칠 수 있는 변수들
- 시간-의존적 위험률을 모델링할 수 있으며, 공변량이 생존 시간에 미치는 영향을 평가하는 데 유용
λ(t∣X)=λ0(t)exp(β1X1+β2X2+⋯+βpXp)
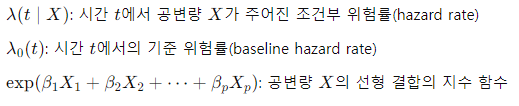
4.2. 코드 전개
import pandas as pd
from lifelines import CoxPHFitter
import matplotlib.pyplot as plt
# 예시 데이터 생성
```
duration: 환자가 생존한 기간(개월 수)
event: 사건 발생 여부(1 = 사망, 0 = 생존)
age: 환자의 나이
treatment: 치료 방법(0 = 치료 A, 1 = 치료 B)
```
data = {
'duration': [5, 6, 6, 7, 8, 8, 10, 12, 14, 15, 18, 20, 25, 5, 7, 12, 13, 14, 16, 20],
'event': [1, 1, 0, 1, 1, 0, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1],
'age': [50, 55, 60, 65, 70, 75, 80, 85, 90, 95, 100, 105, 110, 55, 60, 65, 70, 75, 80, 85],
'treatment': [0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 1]
}
df = pd.DataFrame(data)
# 콕스 비례 위험 모형 적합
cph = CoxPHFitter()
cph.fit(df, duration_col='duration', event_col='event')
# 모형 요약 출력
cph.print_summary()
# 생존 곡선 시각화
cph.plot()
plt.title('Hazard Ratios')
plt.show()
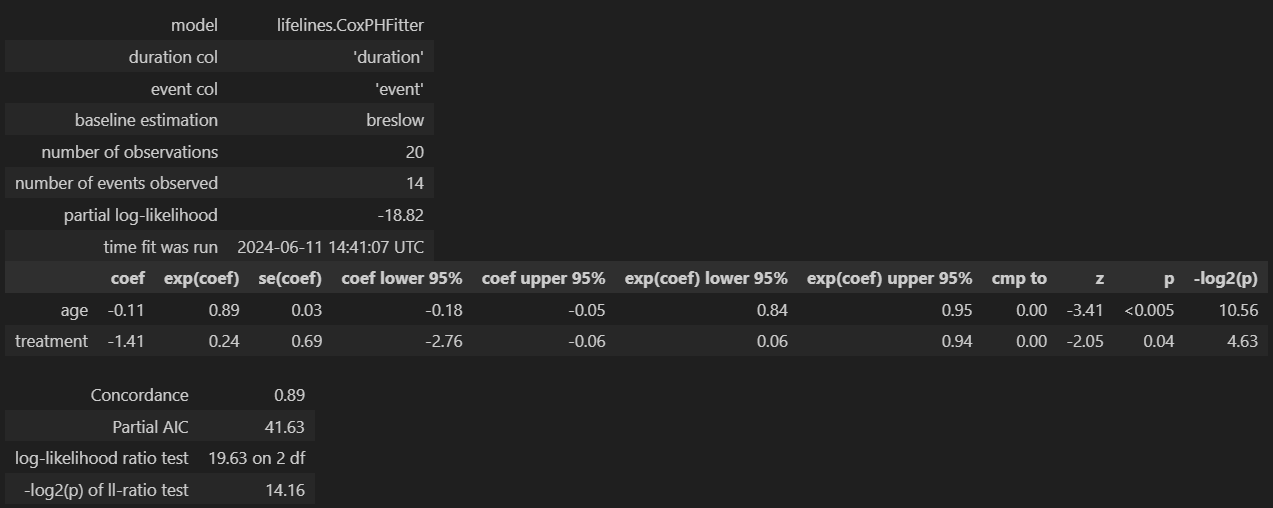
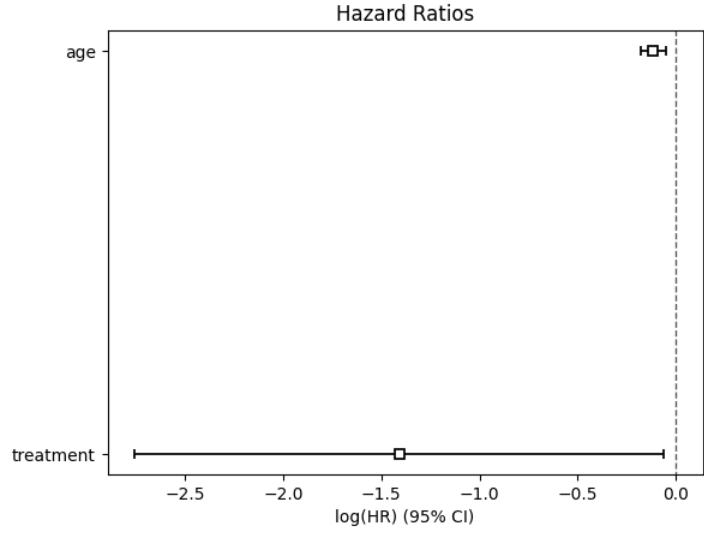
- 결과해석
- age 회귀계수는 -0.11 으로 나이가 증가할 수록 사건의 발생 위험 감소가 감소한다고 해석할 수 있음. 실제로는 exp(-0.11) = 0.89이므로 나이가 1년 증가함에 따라 사망확률이 약 10%씩 감소
- treatment 치료여부는 회귀계수는 -1.41이로 치료를 받은 경우 사건 발생률이 감소한다는 것을 의미함. exp(-1.11) = 0.24이므로 치료를 받은 경우 사망확률이 약 76%씩 감소
- 그래프의 경우 x축은 로그 위험비(log Hazard ratio)를 뜻하며 위험비의 추정값을 말한다. 0보다 작으면 사망위험확률을 낮춰준다고 해석할 수 있으며 age, treatment는 모두 사건 발생비율을 감소시킨다.
- 신뢰구간의 경우 좁을 수록 신뢰도가 높은데 치료의 경우 신뢰구간이 매우 넓어 불확실성이 크다.
5. 최종 정리
- 생존 분석: 다양한 모델링 기법을 포함하는 광범위한 분야로, 시간-이벤트 데이터를 분석
- 카플란-마이어 추정법: 특정 시간까지 이벤트가 발생하지 않을 확률을 추정하는 방법입니다. 사건이 독립적이라는 가정
- Log-Rank 테스트: 두 그룹 간의 시간에 따른 생존율 차이를 검정
- 콕스 비례 위험 모형: 시간에 따른 위험을 모델링하며, 공변량이 시간에 따라 비례적으로 위험률에 영향을 미친다는 가정을 기반
6. SQL 로 생존분석하기
https://www.crosstab.io/articles/sql-survival-curves/
Brian Patrick Kent - How to compute Kaplan-Meier survival curves in SQL
Decision-makers often care how long it takes for important events to happen.
www.crosstab.io
https://sticky-ai.github.io/survival%20analysis/2020/07/29/survival_analysis_kaplan_meier/
Survival Analysis. 카플란-마이어 추정 (Kaplan Meier Estimation)
생존 분석(Survival Analysis)는 시간의 흐름에 따른 어떠한 사건의 발생 확률을 알아보는 통계 분석 및 예측 기법 중 하나입니다. 일반적으로 의료분야에서 특정 수술 방법 혹은 치료 방법에 따른 환
sticky-ai.github.io
반응형
'Data Science' 카테고리의 다른 글
| 2024년 데이터 직군이 나가야 할 방향 정리하기 ft. AI시대 데이터직군 생존 전략 (0) | 2024.08.20 |
|---|---|
| (15) DSforS: Chap7. 7.1 주성분 분석(PCA) (0) | 2024.06.26 |
| DataScience 책 추천(교양, 통계, 데이터과학, 머신러닝, 프로그래밍 등 ) (0) | 2024.06.10 |
| [글또] LLM 관련 모듈 동향 살펴보기- OPEN AI, Langchain , Pandas AI (0) | 2024.03.31 |
| [글또] Google bigquery에 데이터를 적재하고 태블로로 데이터 가져오기 (1) | 2024.03.08 |



